החבילה הסטטיסטית למדעי החברה (SPSS) היא כלי רב עוצמה המשמש חוקרים וסטודנטים כאחד לביצוע ניתוח נתונים מורכב. מדריך SPSS זה נועד לספק סקירה מקיפה של אופן השימוש בתוכנה זו, מתהליך ההורדה הראשוני ועד ביצוע ניתוח סטטיסטי מעמיק. לפני שנעמיק בנבכי SPSS, חשוב לציין שלעיתים קרובות ניתן להוריד את התוכנה בחינם מאתר המוסד שלכם. זהו יתרון משמעותי לסטודנטים וחוקרים הפועלים בתקציב. הקפד לבדוק את המשאבים של המוסד או מחלקת הסטודנטים שלך כדי לקבל גישה להורדה של SPSS. לאחר שהורדת והתקנת את SPSS בהצלחה, הגיע הזמן להכיר את הממשק שלו. SPSS תוכנן להיות ידידותי למשתמש, עם פריסה ברורה ואינטואיטיבית. הקדישו זמן לחקור את התפריטים והאפשרויות השונות העומדות לרשותכם.
הזנת נתונים הוא היבט בסיסי של SPSS. תצטרך להבין כיצד להזין את הנתונים שלך בצורה נכונה כדי להבטיח תוצאות מדויקות. זה כולל יצירת משתנים המייצגים את הנתונים שלך והזנת ערכי הנתונים עבור כל משתנה. בנוסף, SPSS מאפשר לך להגדיר ולנהל נתונים חסרים או שגויים, מה שמבטיח את שלמות הניתוח שלך.
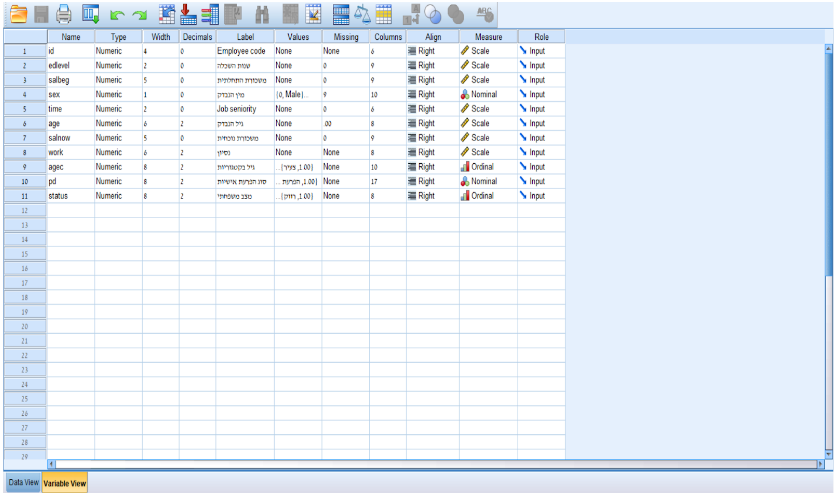
חלון תצוגת המשתנים ב-SPSS הוא המקום שבו אתה מגדיר את המשתנים שלך. כל שורה בתצוגה זו מייצגת משתנה אחר, וכל עמודה מייצגת תכונה אחרת של המשתנה. נסקור את העמודות הכי חשובות:
Name: כאן אתה מזין את שם המשתנה. שמות משתנים ב-SPSS חייבים להתחיל באות ואינם יכולים להכיל רווחים או תווים מיוחדים.
Type: זה מגדיר את סוג הנתונים שהמשתנה יכול להחזיק. הערך יכול להיות מספרי, מחרוזת (טקסט), תאריך ואחרים. סוג הנתונים שתבחר ישפיע על סוג הניתוחים שתוכל לבצע עם המשתנה.
Label: כאן ניתן לספק שם ארוך ותיאורי יותר למשתנה. למשל, עבור פריטי שאלון ניתן לכתוב את מלל השאלה הרלוונטית.
Values: זהו המקום שבו ניתן להגדיר תוויות ערך עבור משתנים מקודדים. לדוגמה, אם יש לך משתנה שבו 1 מייצג "זכר" ו-2 מייצג "נקבה", תוכל להגדיר אותם בעמודת הערכים.
Missing: זהו המקום שבו אתה יכול להגדיר לאילו ערכים יש להתייחס כנתונים חסרים בניתוח שלך. למשל, אם תרצה שהערך 9 יייצג ערך חסר או נבדקים שסימנו אופציית "לא יודע" בשאלון.
Measure: כאן ניתן להגדיר את רמת המדידה של המשתנה. היא יכולה להיות נומינלית (קטגוריות), אורדינלית (סדר/דירוג) או סקאלה (רציף). המדד שתבחר ישפיע על איזה סוג של ניתוחים תוכל לבצע עם אותו המשתנה. הבנת האפשרויות הללו בתצוגת המשתנה היא חיונית לניהול נתונים יעיל ב-SPSS. באמצעות חלון זה, תוכל להגדיר את הפרמטרים של הנתונים שלך ולהבטיח שהניתוחים שלך מתבצעים בצורה נכונה.
SPSS מציע מגוון רחב של בדיקות ונהלים סטטיסטיים, המאפשרים לך לבצע ניתוח מעמיק של הנתונים שלך. החל מחישוב ציונים ממוצעים ועד ביצוע מבחנים סטטיסטיים מורכבים, SPSS מספק את הכלים הדרושים לך כדי לפרש את הנתונים שלך ביעילות. זכור, הבנת הבדיקה הסטטיסטית המתאימה לשימוש חשובה לא פחות מהידע כיצד לבצע אותה ב-SPSS. בואו נעבור על כמה מהניתוחים הנפוצים ביותר:
סטטיסטיקה תיאורית: פרוצדורה זו כוללת הצגת מדדים כגון ממוצע, חציון, מצב, סטיית תקן וטווח. אתה יכול למצוא אותם בתפריט "Analyze", לאחר מכן בחר "Descriptive Statistics", ולבסוף "Descriptives".
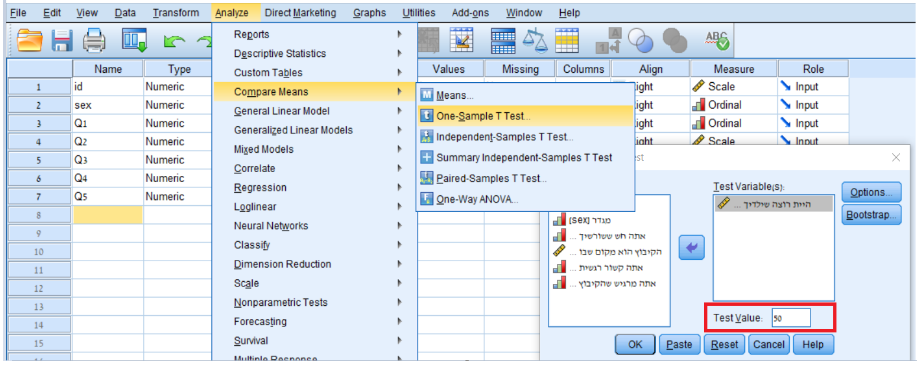
מבחני T: אלה משמשים להשוואת הממוצע של מדגם בודד לממוצע אוכלוסייה או השוואת הממוצע של שתי קבוצות (תלויות או בלתי תלויות). ניתן לבצע מבחן t למדגם בודד על ידי מעבר לתפריט "Analyze" > "Compare Means", ולבסוף "Independent samples T-test" או "Paired T-test" בהתאם לנתונים שלך או "One Sample T-test" עבור השוואת ממוצע מדגם אחד לממוצע אוכלוסייה.
מבחן T למדגם בודד : בחלונית ה Test Value- יש לכתוב את הערך המשוער של ממוצע האוכלוסייה אליו רוצים להשוות את ממוצע המדגם. בחלונית הTest Variable(s)- , יש להוסיף את המשתנה התלוי ברמת הScale.
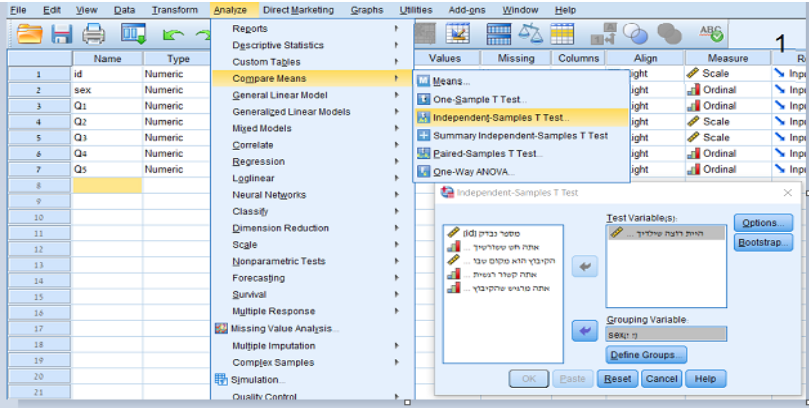
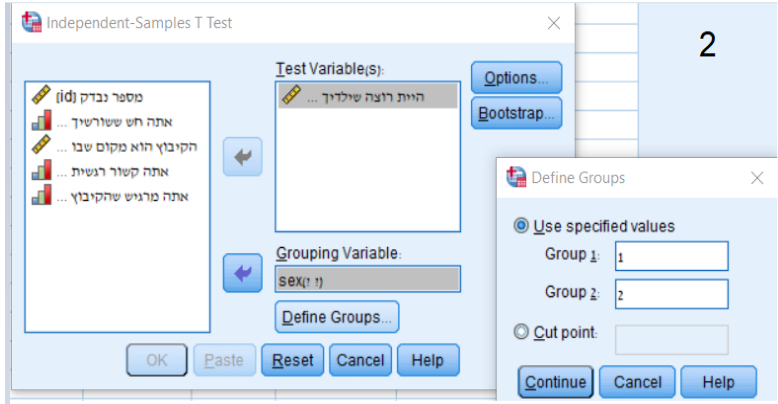
מבחני T בלתי תלויים: בחלונית הGrouping Variables- יש להוסיף את המשתנה הב"ת ברמת Nominal ולאחר מכן להגדיר את קוד הקבוצות הנבדקות. בחלונית הTest Variable(s)- , יש להוסיף את המשתנה התלוי ברמת הScale.
ב-SPSS, מה שיעניין אותנו להסתכל עליו זה רק ערך ה-"Sig" (מובהקות) ודרגות החופש (df). אם ערך ה-Sig נמוך מ-0.05, משמעות הדבר הוא שהממוצע שונה באופן מובהק מהערך הידוע. שימו לב: ערך ה-Sig בפלט הוא תמיד דו זנבי. משמע, אם ההשערה בשאלה היא חד זנבית, יש לחלק אותו ב-2 על מנת להחזיר אותו לערך חד זנבי.
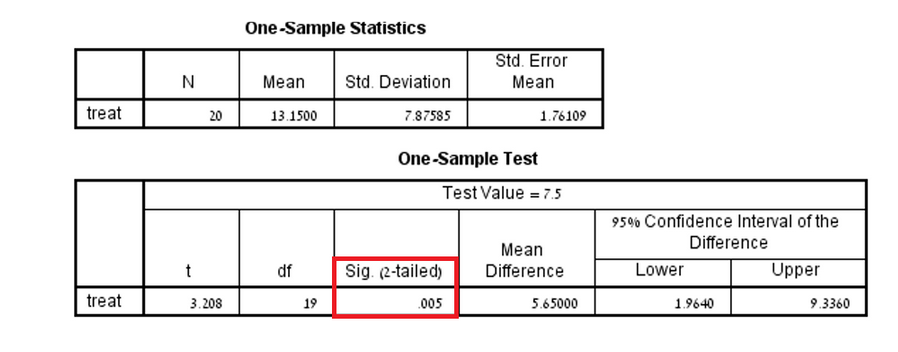
מבחני T תלויים/מזווגים: בחלונית הTest Variable(s) , יש להוסיף את שני המשתנים הנבדקים, אחד יהיה משתנה הבדיקה "לפני" והשני יהיה משתנה הבדיקה "אחרי".
מבחן t למדגמים מזווגים ישמש אותנו כאשר יהיו לנו שתי קבוצות תלויות של לפני ואחרי, ונרצה לדעת האם הממוצעים של שתי הקבוצות הללו שונים באופן מובהק לפני ואחרי המדידה. בפלט אנו נסתכל על מספר חלקי מידע מרכזיים:
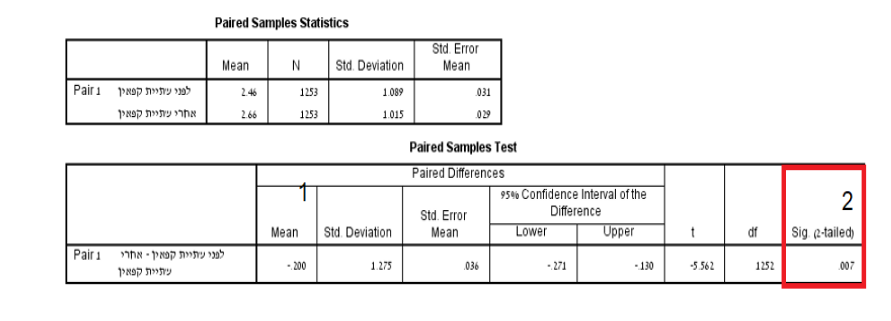
הבדלים מזווגים (Paired Samples Statistics): חלק זה של טבלת הפלט מספק נתונים סטטיסטיים תיאוריים (ממוצע, סטיית תקן, ממוצע טעויות תקן) עבור ההבדלים בין שתי קבוצות התצפיות.
ערך ה-t: זהו ערך סטטיסטי המבחן עבור מבחן ה-t ומייצג את גודל ההפרש ביחס לנתונים שלנו.
df: אלו דרגות החופש, המחושבות כמספר זוגות התצפיות פחות 1 (n-1).
Sig. (דו זנבי): זהו ערך ה-p. אם ה-Sig נמוך מ-0.05, אזי ניתן להסיק שההבדל בין שתי קבוצות התצפיות נחשב מובהק סטטיסטית. יש לחזור אל ממוצעי הקבוצות בכדי לקבוע איזה מן הקבוצות יותר גבוהה באופן מובהק מהשנייה.
כעת בואו נפרש את הפלט על סמך הנתונים שסופקו:
ניתן לראות שהפלט משווה בין שני תנאים, לפני ואחרי שתיית קפאין. בטבלה העליונה ("Paired Samples Statistics"), אנו רואים שהציון הממוצע לפני שתיית קפאין הוא 2.46 ואילו אחרי שתיית קפאין הוא 2.66, וגודל המדגם (N) עבור שני התנאים הוא 1253. בטבלה התחתונה ("Paired Samples Test"), ניתן לראות את התוצאות של מבחן ה-t:
ההבדל הממוצע בין שני התנאים הוא 0.2–. ערך שלילי זה מצביע על כך שבממוצע, הציונים היו נמוכים יותר לפני שתיית קפאין מאשר לאחר מכן. ערך t הוא 5.562-. ערך זה הוא שלילי, אשר מתיישר עם ההבדל הממוצע השלילי , מה שמצביע על כך שהציונים היו בדרך כלל נמוכים יותר לפני שתיית קפאין. דרגות החופש (df) הן 1252, אשר מחושבות כמספר זוגות התצפיות הכלליות (1253) פחות 1. ערך ה-Sig במקרה הנוכחי הוא 0.007. מכיוון שערך זה קטן מ-0.05, אנו יכולים להסיק שההבדל בין שני התנאים הוא מובהק סטטיסטית. לכן, בהתבסס על פלט זה, אנו יכולים להסיק שלשתיית קפאין השפעה חיובית מובהקת על המשתנה הנמדד, כאשר הציונים עולים בדרך כלל לאחר צריכת קפאין.
קטגוריה זו משמשת להשוואת הממוצעים של יותר משתי קבוצות באמצעות מבחן ANOVA, אשר משווה בין הממוצעים של יותר משתי קבוצות.
ניתן למצוא ניתוח זה בתפריט "Analyze" > "Compare Means > "One way ANOVA" . בחלונית ה-Factor יש להוסיף את המשתנה הב"ת ברמת Nominal או Ordinal ובחלונית ה-Dependent List יש להוסיף את המשתנה התלוי ברמת Scale. בפלט, אנו נראה שני סוגים של דרגות חופש (df): "df between groups" ו-"df within groups". ה-df "בין קבוצות" ("between") יחושב על ידי מספר הקבוצות פחות אחת (J-1). כמו כן, ה-df "בתוך הקבוצות" ("within") יחושב על ידי החסרת המספר הכולל של התצפיות במספר הקבוצות (N-J). אם ערך ה-Sig. יימצא נמוך מ-0.05, משמעות הדבר היא שלפחות קבוצה אחת שונה משמעותית מהאחרות. במידה והדבר הוא נכון, יש לבצע ניתוחי המשך (Post Hoc) בשביל להבין מי מבין הקבוצות שונה משמעותית מהאחרות, עליהם לא נרחיב במאמר זה.
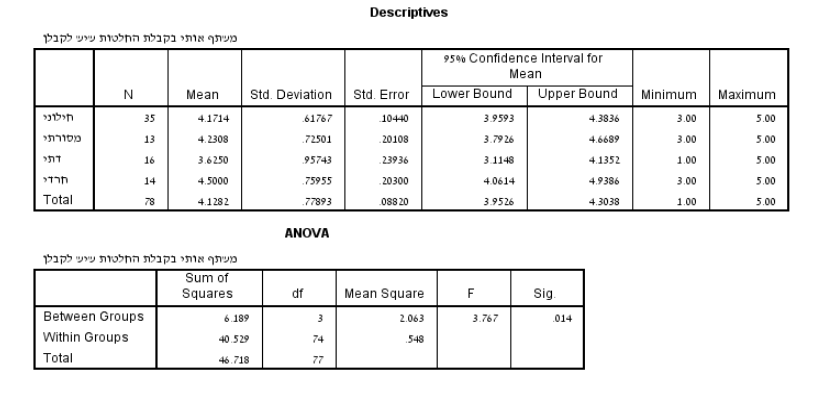
הפלט מעל הוא ממבחן ANOVA המשווה בין ארבע קבוצות: חילוני , מסורתי, דתי וחרדי. משתנה העניין (המשתנה התלוי) הוא הסכמה עם ההצהרה לפיה "הבן שלי משתף אותי בקבלת החלטות". בטבלת הסטטיסטיקה התיאורית, אנו יכולים לראות את הציונים הממוצעים עבור כל קבוצה. הקבוצה עם הציון הממוצע הגבוה ביותר היא 'חרדי' עם ממוצע של 4.50, והקבוצה עם הציון הממוצע הנמוך ביותר היא 'דתי' עם ממוצע של 3.62. בטבלת "ANOVA", אנו רואים את התוצאות של המבחן:
סכום הריבועים (SS):
1. סכום הריבועים "בין הקבוצות" (SSB) ששווה 6.189, עם 3 דרגות חופש (df) . דרגות החופש מחושבות ע" החסרת מספר הקבוצות (4) ב-1.
2. סכום הריבועים "בתוך הקבוצות" ששווה 40.529, עם 74=df. במקרה הנוכחי, דרגות החופש מחושבות על ידי מספר התצפיות הכולל (78) פחות מספר הקבוצות (4).
אומדני השונויות וערך ה-F:
זהו סטטיסטי המבחן עבור ה-ANOVA, והוא מייצג את היחס (חלוקה) בין אומדן השונויות "בין הקבוצות" (2.063) לאומדן השונויות "בתוך קבוצות" (0.548). החלוקה בין שתי אומדני השונויות הללו, תביא לנו את ערך ה-F שהוא 3.76.
מובהקות התוצאה:
ערך ה-Sig מייצג את הp-value (ערך הp). מכיוון שערך הSig נמוך מ-0.05 (0.014<0.05), אנו יכולים להסיק שישנו הבדל מובהק בין לפחות שתיים מהקבוצות (חילוני, מסורתי, דתי, חרדי), במידה שבה הם מרגישים שהבן שלהם מערב אותם בקבלת ההחלטות.
מתאם (פירסון וספירמן):
מדדי קשר אלו משמשים למדידת הקשר בין שני משתנים בסולם Scale (עבור פירסון) או סולם Ordinal (עבור ספירמן). ניתן לבצע ניתוח מתאם על ידי מעבר לתפריט "Analyze" > "Correlation" > "Bivariate". לאחר מכן, בוחרים למטה את המתאם המתאים (פירסון או ספירמן) בהתאם לסוג המידע שקיים.
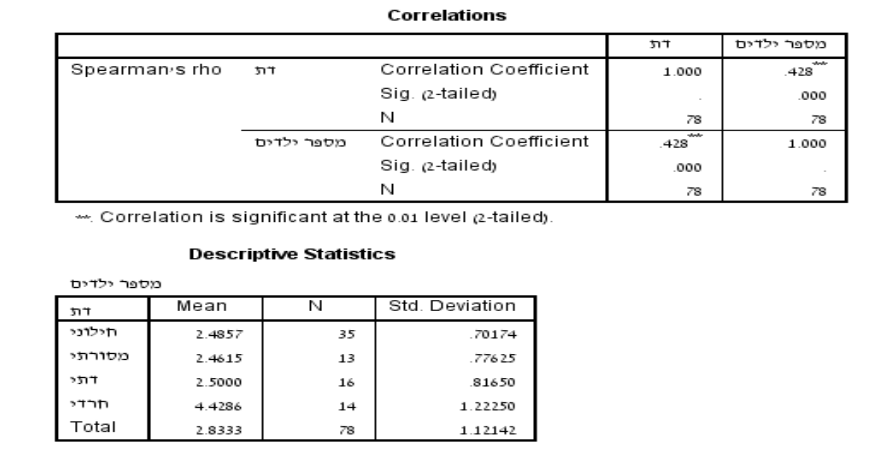
פלט זה הוא של מתאם ספירמן, שהוא מבחן המשמש למדידת החוזק והכיוון של הקשר המונוטוני כאשר לפחות אחד מהמשתנים הוא אורדינלי. שני המשתנים במקרה זה הם דת (משתנה אורדילנלי/סדר) ומספר ילדים (משתנה בסולם רווח/מנה). בטבלה הראשונה (Correlations), אנו רואים את התוצאות של מבחן המתאם של Spearman:
מקדם המתאם בין רמת הדתיות למספר ילדים הוא 0.428. ערך זה נע בין 1 ל1–, כאשר 1– מצביע על מתאם שלילי מושלם, 1 מציין מתאם חיובי מושלם ו-0 מציין שאין מתאם. ערך של 0.428 מצביע על מתאם חיובי בעוצמה בינונית בין שני המשתנים. כאשר ערך הSig. קטן מאוד (<0001.), יופיע שהוא שווה 0.000. מכיוון שערך זה קטן מ-0.05, אנו יכולים להסיק שהמתאם הוא מובהק סטטיסטית. לכן, בהתבסס על פלט זה, ניתן להסיק שישנו מתאם חיובי מובהק בעוצמה בינונית בין דת למספר ילדים. הדבר מצביע על כך שככל שרמת הדתיות עולה, כך גם מספר הילדים בממוצע נוטה לעלות.
בטבלה השנייה (Descriptive Statistics) אנו רואים את מספר הילדים הממוצע עבור כל קבוצה דתית. הקבוצה עם מספר הילדים הממוצע הגבוה ביותר היא 'חרדי' עם ממוצע של 4.43. מספר הילדים הממוצע של שאר הקבוצות, 'חילוני', 'מסורתי', "דתי' הם 2.46 עד 2.50 בקירוב, ממצאים אשר תומכים בתוצאת המתאם.
רגרסיה
ניתן לבצע רגרסיה על מנת לנבא את הערך של משתנה אחד על סמך הערך של אחר. אפשר לבצע ניתוח רגרסיה על ידי מעבר לתפריט "Analyze" > "Regression" > "Linear". ניתן להשתמש ברגרסיה על מנת לנבא משתנה תלוי אחד באמצעות משתנה בלתי תלוי אחד או בעזרת כמה משתנים בלתי תלויים (רציפים או קטגוריאליים).
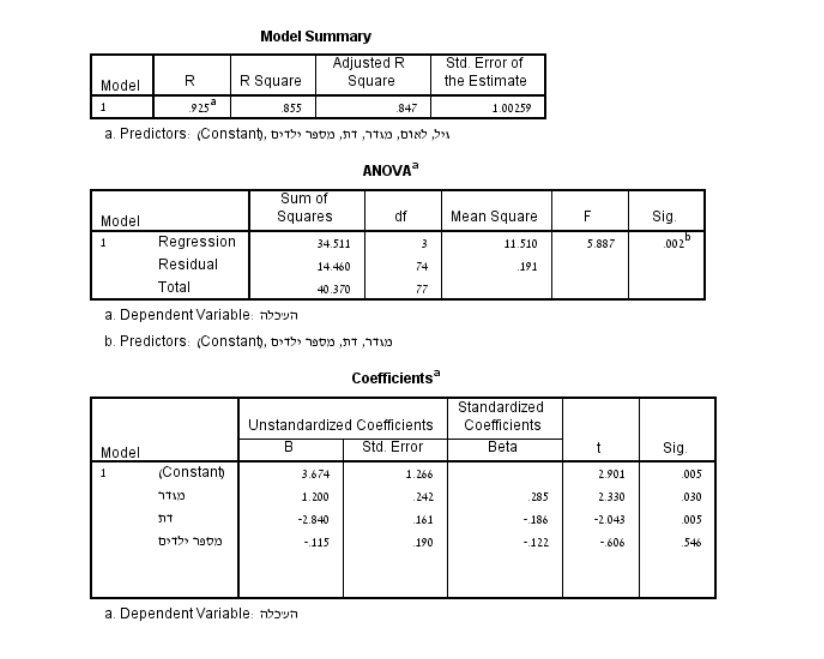
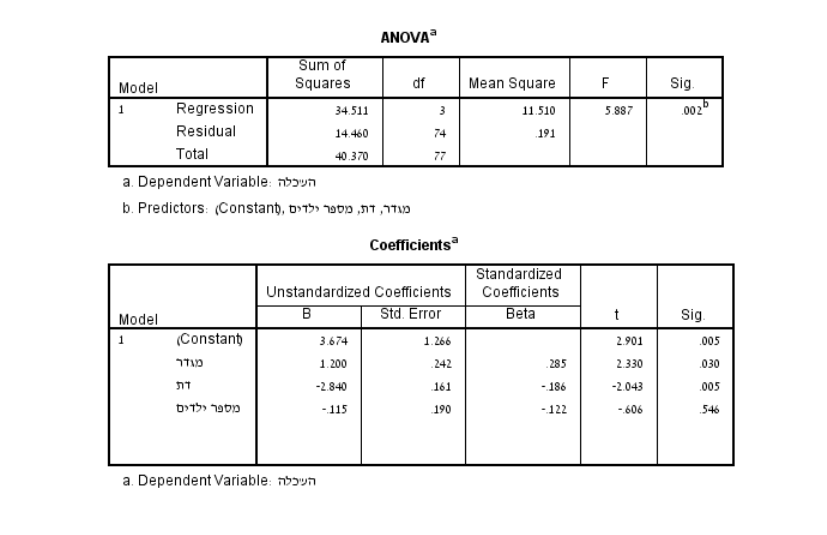
פלט זה הוא מניתוח רגרסיה מרובה. הוא משמש אותנו להבין כיצד מספר משתנים בלתי תלויים (מגדר, דת ומספר ילדים) קשורים (מנבאים) למשתנה התלוי (השכלה). בטבלה הראשונה (ANOVA) אנו רואים את התוצאות של מודל הרגרסיה הכללי:
סכום ריבועי הסטיות (SS):
סכום ריבועי סטיות הרגרסיה (SSreg) הוא 34.511, עם 3 דרגות חופש (df) שמחושב כמספר המנבאים במודל. סכום ריבועי סטיות הטעות (SSres) הוא 14.460, עם df=74. דרגות חופש אלו מחושבות כמספר התצפיות הכולל (78) פחות מספר המנבאים (3) פחות 1.
אומדני שונויות וערך ה-F:
ערך ה- F הוא 5.887, וערך ה-Sig הוא 0.002. את ערך ה-F אנו מקבלים על ידי חלוקת אומדן שונויות הרגרסיה (MSreg; 11.51) באומדן שונויות הטעויות (MSres; 0.191) . מכיוון שערך ה-Sig קטן מ-0.05, אנו יכולים להסיק שמודל הרגרסיה מובהק סטטיסטית. בטבלת "Coefficients", אנו רואים את התוצאות עבור כל מנבא:
המקדמים הבלתי מתוקננים (B):
מייצגים את השינוי במשתנה התלוי עבור כל שינוי של יחידה אחת במנבא, בהנחה שכל שאר המנבאים מוחזקים קבוע (כלומר לא משפיעים). לדוגמה, ערך B עבור מספר ילדים הוא 0.115-, מה שמרמז שרמת השכלה יורדת ב0.115 יחידות בממוצע עבור כל ילד שמתווסף למשפחה, בהנחה שמגדר ודת מוחזקים קבוע. אולם, ניתן לראות בעמודת ה-Sig כי מנבא זה אינו מובהק שכן הערך שלו (0.546) גבוה מרמת המובהקות שאנו משתמשים בה בד"כ (0.05).
המקדמים המתוקננים (Beta):
מייצגים את השינוי במשתנה התלוי (המנובא) במונחים של סטיות תקן, עבור כל שינוי סטיית תקן אחד במשתנה הבלתי התלוי (המנבא). המקדמים הללו שימושיים להשוואת העוצמה היחסית של מנבאים שונים. לדוגמה, ערך הבטא עבור מגדר הוא 0.285, שהוא גדול יותר מערכי הבטא עבור דת ומספר ילדים (בערך מוחלט), מה שמצביע על כך שלמגדר יש קשר חזק יותר עם השכלה כאשר כל המנבאים מוחזקים קבוע.
ערך t:
הוא סטטיסטי המבחן עבור כל מנבא בשביל לבדוק את מובהקות הניבוי. כמו שניתן לראות בפלט באמצעות עמודת ה-Sig, ערכי ה-t עבור משתני המגדר ודת הינם מובהקים, בעוד שמספר ילדים לא. לכן, בהתבסס על פלט זה, אנו יכולים להסיק שמגדר ודת מנבאים מובהקים של השכלה, בעוד שמספר ילדים לא.
אחוז שונות מוסברת (R בריבוע):
הערך R בריבוע, הידוע גם כאחוז השונות המוסברת, הוא מדד סטטיסטי המייצג את שיעור או אחוז השונות עבור המשתנה התלוי אשר מוסבר על ידי משתנה או משתנים בלתי תלויים במודל רגרסיה. בהקשר של הנתונים, ניתן להסתכל בטבלת ה "Model Summary" ונמצא שערך הוא 0.855. משמעות הדבר היא ש-85.5% מהשונות (ההבדלים) בהשכלה ניתנים להסבר על ידי המשתנים מגדר, דת ומספר ילדים יחד. ניתן להסתכל על עמודת ה-R בשביל להבין טוב יותר האם את עוצמת אחוז השונות המוסברת. במאמר שלנו על מדדי קשר עברנו על מה נחשב עוצמת קשר חזקה, חלשה ובינונית.
במדריך מקיף זה, חקרנו באופן מעמיק את אופן הניתוח הסטטיסטי באמצעות SPSS של המבחנים השונים שניתן לבצע באמצעות תוכנה זו. הבנו כיצד ניתן להזין נתונים לתוך הSPSS, להגדיר משתנים ומהי המשמעות של הבנת תכונות שונות של משתנים. מדריך זה כיסה גם מגוון רחב של ניתוחים סטטיסטיים שניתן לבצע באמצעות SPSS, כגון סטטיסטיקה תיאורית, מבחני T, ANOVA (תלויים ובלתי תלויים), מתאמים ורגרסיה והבנו אותם באמצעות דוגמאות מהעולם האמיתי. עבור כל סעיף עברנו על פרשנויות מפורטות כדי להבטיח שתוכלו לא רק לבצע ניתוחים אלה אלא גם להבין אותם. אז קדימה, צללו לתוך הנתונים, וראו אילו תובנות תוכלו לחשוף עם SPSS. ניתוח שמח!