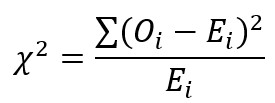התחבר/הירשם

מה הקשר? המדריך למדדי הקשר: פירסון, ספירמן וחי בריבוע

מה הקשר?! מתאם פירסון, ספירמן, חי בריבוע וקרמר

מבוא: מהו מקדם מתאם?

מקדם המתאם הוא מדד סטטיסטי לעוצמת הקשר ליניארי בין שני משתנים ויסומן באות r. הערכים של המתאם יכולים לנוע בין 1 (מתאם חיובי מושלם) למינוס 1 (מתאם שלילי מושלם) וביניהם יש את הערך 0 אשר אומר לנו שלא קיים קשר ליניארי בכלל. במתאם פירסון וספירמן, מתאם חיובי מייצג מצב שבו ערכים בסדרה אחת, גוררים עלייה בערכים של סדרה אחרת, ולהפך. מתאם שלילי לעומת זאת, מייצג מצב שבו עלייה בערכים של סדרה אחת, גורר ירידה בערכים של סדרה אחרת.  מקדמי המתאם משמשים אותנו על מנת להעריך את מידת הקשר בין שני משתנים, גורמים או מערכי נתונים. לדוגמה, עלייה של שכר בעקבות עלייה במספר שנות השכלה, מייצג קשר חיובי. מתאם פירסון ומתאם ספירמן מורכבים גם מהכיוון (חיובי או שלילי) וגם מהעוצמה (חלש/בינוני/חזק/מושלם). לעומת זאת, מתאם חי בריבוע וקרמר, אשר משמשים למדידת קשר בין משתנים קטגוריים, תמיד יהיו חיוביים. כלל אצבע הוא שמתאם מתחת ל0.3 נחשב למתאם חלש, מתאם בין 0.3 ל0.6 נחשב בינוני, מתאם מ0.6 ומעלה נחשב חזק וכאשר המתאם שווה ל1, הוא מייצג קשר מושלם.

מהם המקדמים הקיימים?

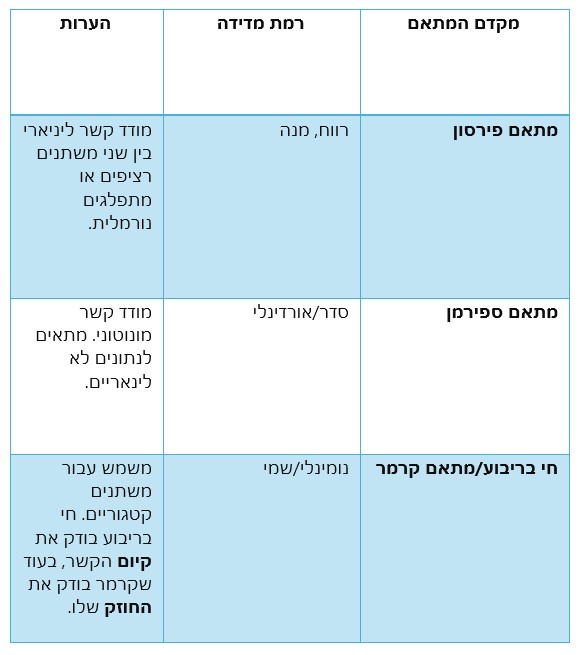
קיימים ארבעה מדדי קשר נפוצים שאנו נשתמש בהם: פירסון (r), ספירמן (rs), קרמר (rc) וחי בריבוע (χ2). את מדד הקשר המתאים נוכל לבחור לפי סולם המדידה המתאים של המשתנים. בטבלה להלן מרוכזים מדדי הקשר לפי סולם המדידה המתאים לו:

משתנה שמי (מתאם חי בריבוע/קרמר)

אם שני המשתנים שלנו בסולם שמי (Nominal) , המדד המתאים לבחינת הקשר ביניהם הוא מבחן חי בריבוע (לבדיקת מובהקות הקשר) ומתאם קרמר (לבדיקת עוצמת הקשר). מבחן חי ריבוע משווה בין השכיחויות הנצפות (Observed) בנתונים מסוימים לבין השכיחויות שהיינו מצפים למצוא (Expected), אילו לא היה קשר בין המשתנים. הנוסחה לחישוב חי בריבוע היא:

כאשר:

Oi = שכיחות נצפית (Observed) עבור תא מסוים בטבלה

Ei= שכיחות צפויה (Expected) עבור תא מסוים בטבלה. 

הנוסחה כוללת בתוכה את סכום ההפרש בריבוע בין הObserved לExpected, חלקי שכיחות הExpected עבור כל תא של המשתנים הקטגוריים. 

שאלה לדוגמא חי בריבוע

חוקרים בדקו את הקשר בין הרגלי פעילות גופנית (כן/לא) לבין איכות השינה (טובה/רעה) במדגם של 100 אנשים, ונאספו את הנתונים הבאים:

 

מכיוון שיש לנו משתנים שמיים-קטגוריים, עלינו להשתמש במדד חי בריבוע בכדי לחשב את קיומו של הקשר ביניהם. על מנת לחשב את חי בריבוע, ראשית עלינו לחשב את השכיחויות הצפויות (Expected) עבור כל תא בטבלה. שכיחות הExpected עבור כל תא מחושבת על ידי הכפלת הסה"כ של אותה שורה בסה"כ של אותו טור ולאחר מכן חלוקה בסך הכל הכולל. בואו נחשב לדוגמא עבור תא אחד (שינה טובה וכן פעילות גופנית) על מנת להבין כיצד מחשבים:

משמעות המספר הזה הוא שאילו לא היה קשר בין פעילות גופנית לשינה, היינו מצפים למצוא 30 נבדקים שכן ביצעו פעילות גופנית וישנו טוב. 

בטבלה מטה, ניתן לראות את כל שכיחויות הExpected:

כעת ניתן לחשב את מדד החי הריבוע:

 

מובהקות חי בריבוע

לאחר שחושב החי בריבוע, נוכל לבדוק האם הקשר שהוא בודק, אכן מובהק או לא. על מנת לעשות זאת, עלינו להסתכל בטבלת חי בריבוע לערכים קריטיים, ברמת המובהקות המתאימה (נניח 5%) ולהצליב עם דרגות החופש המתאימות. במקרה של חי בריבוע, דרגות החופש מחושבות על ידי מספר הרמות (אפשרויות) של המשתנה הראשון פחות 1 כפול,  מספר האפשרויות של המשתנה השני פחות 1. במקרה הנוכחי, מכיוון שלכל משתנה שתי אפשרויות בלבד, דרגות החופש המתאימות הן 1. בטבלה מטה ניתן לראות שאם נצליב את דרגות החופש האלו עם רמת המובהקות שבחרנו, נקבל ערך קריטי של 3.841:  

 

כמו במבחן זד, כאשר הערך הסטטיסטי (המחושב) גדול מהערך הקריטי, אנו נדחה את השערת האפס ונסיק על קיומו של קשר.

מתאם קרמר (Cramer's V)

ה-V של Cramér הוא מדד לבדיקת עוצמת הקשר בין שני משתנים נומינליים (קטגוריים), ונע בין 0 ל-1. מדד זה נגזר מהסטטיסטי של חי ריבוע ומחושב כך:

 

* כאשר L הוא המספר הנמוך מבין השורות או הטורים.

אם נמשיך את הדוגמא שלנו ממקודם, מתאם קרמר יהיה:

מכאן אנו יכולים להבין שאמנם קיים קשר מובהק בין פעילות גופנית (כן/לא) לבין איכות שינה (טובה/רעה), אך בעוצמה חלשה.

משתנה בסולם סדר/אורדינלי (מתאם ספירמן)

 במידה וסולם המדידה של לפחות אחד המשתנים הנו סדר ומעלה או שהקשר בין המשתנים לא לינארי , אלא מונוטוני, או שידוע לנו שאחד מהמשתנים לא מתפלג נורמלית באוכלוסייה, נבחר במתאם ספירמן. מתאם ספירמן מבוסס על תכונת הסדר של המספרים. קשר מונוטוני בוחן האם ככל ש-x גדל, כך גם y גדל, אך אין חשיבות לכמות שבה כל אחד מהמשתנים גדל. 

מתאם ספירמן דומה למבחנים הא-פרמטרים אשר עושים שימוש בתכונת הסדר של המספרים בעזרת דירוג הערכים. כאשר נרצה לחשב את מתאם ספירמן אנו נעבוד עם נוסחת המתאם של ספירמן אשר עושה שימוש בדירוגים של המספרים. מכאן אנו מבינים שהצעד הראשון שעלינו לבצע כאשר נחשב את מתאם ספירמן הוא חישוב הדירוגים של התצפיות. בתצוגה מטה,  ניתן לראות כיצד נראים עוצמות וכיוונים שונים של מתאם ספירמן. 

כמו שאתם רואים בתמונות, עבור קשר חיובי: קשר מונוטוני מושלם משמעו שברגע ש-X עולה, גם Y עולה יחד איתו תמיד (אך לא בהכרח באותה פרופורציה). עבור קשר שלילי, המקרה הוא בדיוק הפוך: כאשר X עולה, Y יורד תמיד. בשני הכיוונים (חיובי ושלילי), עצמת הקשר נפגעת כאשר ישנן תצפיות שחורגות מהדפוס הקבוע הזה של הקשר המונוטוני. ככל שהדפוס הזה נפגע יותר, כך גם עוצמת הקשר נפגעת. לאחר שנדרג את התצפיות מהקטן לגדול,  נוכל לחשב את מתאם ספירמן באמצעות שימוש בנוסחה הבאה:

הנוסחה סוכמת/מחברת את ההפרש בריבוע של דירוגי התצפיות (d) ומחלקת במספר התצפיות. תצפיות בעלי ערך זהה, יקבלו את הדירוג הממוצע בין המיקום המספרי שלהם. כך לדוגמא, עבור סדרת המספרים הבא: 1,2,4,4,5,7 , נדרג את התצפיות באופן הבא: 1,2,3.5,3.5,4. אתם יכולים לראות שהערך '4' קיבל את הדירוג 3.5 מכיוון שהוא נמצא במקום הרביעי והחמישי (ולכן הדירוג שלו יהיה האמצע ביניהם). בואו נראה דוגמא לשאלה כדי שנוכל להבין טוב יותר את השימוש בנוסחה.

שאלה לדוגמא מתאם ספירמן

במחקר שמטרתו להבין את הקשר בין פעילות גופנית לכמות שעות שינה בלילה, חוקר אסף נתונים מ-6 מתנדבים. המשתתפים התבקשו לרשום את מספר השעות שהם השקיעו בפעילות גופנית ואת מספר השעות שישנו בכל לילה במשך שבוע. החוקר שיער שככל פעילות גופנית מרובה קשורה ליותר שעות שינה. בהתבסס על הנתונים מטה, בדוק את הקשר בין שעות פעילות גופנית לשעות שינה. הנח שהנתונים באוכלוסייה אינם מתפלגים נורמלית.

פתרון

מכיוון שנתבקשנו לבדוק קשר בין המשתנים ונתון לנו שהנתונים לא מתפלגים נורמלית באוכלוסייה,  אנו מבינים שמדובר במתאם ספירמן. על מנת לפתור את התרגיל, ראשית עלינו קודם לסדר את התצפיות מהקטן לגדול עבור X ועבור Y ונדרג אותם מ1-6 (באדום): 

שעות שינה (X):

  5.5 (1) ,6 (2.5), 6 (2.5), 7 (3.5),7 (3.5),8 (6)

שעות פעילות גופנית (Y)

 0.5 (1) ,1(2) ,1.5 (3),2 (4) ,3 (4.5), 3 (4.5) 

כעת, למען הנוחות שלנו, נחליף את הטבלה עם הערכים המקוריים עם ערכי הדירוג של התצפיות, ונוסיף עוד עמודה של הפרש הדירוגים (d):

כעת נוכל לחשב את מתאם ספירמן על ידי הצבה בנוסחה:


אז כמו שאנחנו רואים, קיבלנו מתאם ספירמן חיובי בעוצמה חזקה. משמעות הדבר היא שככל ששעות פעילות הגופנית עולות, שעות השינה עולות, ולהפך.

משתנה בסולם רווח/מנה (מתאם פירסון)

מתאם פירסון משמש לניתוח החוזק והכיוון של הקשר הליניארי בין שני משתנים. מתאם זה עוזר לנו לכמת את המידה שבה שני משתנים קשורים זה לזה באופן ליניארי ויסומן באות 'r'. הערכים של פירסון נעים בין 1 ל-1, כאשר r=1 מציין קשר ליניארי חיובי מושלם (ככל ש-x עולה, y עולה ובאותה פרופורציה), וr=-1 מציין קשר ליניארי שלילי מושלם ככל ש-x עולה, y יורד ובאותה פרופורציה). r=0 מציין שאין קשר ליניארי בין המשתנים (ככל ש-x עולה, y עולה או יורד, ללא קשר לx). לדוגמה, אילו רמות השכלה ייקשרו להכנסה גבוהה יותר, ניתן לומר שקיים בין המשתנים הללו קשר חיובי. בתמונות למטה, תוכלו לראות כיצד ניתן לזהות בגרף כל אחד מעוצמות וכיווני הקשר של פירסון: 

 .

כפי שאתם רואים, כאשר מתאם פירסון הוא מושלם (חיובי או שלילי), כל נקודות התצפיות מסתדרות באופן מושלם על קו המתאם. אולם, כאשר המתאם הוא לא מושלם, ניתן לראות שחלק מהתצפיות חורגות מקו המתאם. לעומת זאת, כאשר התצפיות מפוזרות באופן רנדומלי, לא ניתן להעביר קו אחד שיסביר את המגמה של ההשתנות המשותפת של X וY ולכן, הקו שנעביר יהיה קו אופקי ישר שיציין את היעדר הקשר.

חישוב מתאם פירסון

על מנת לחשב את מתאם פירסון, עלינו להשתמש בנוסחה הבאה:

החישוב כולל שלושה שלבים: 

1. חישוב ציוני סטייה: עבור כל זוג תצפיות, אנחנו נחסיר כל תצפית מ-X בממוצע שלה, ונעשה את אותו הדבר עבור משתנה Y. 

2. הכפלה של כל אחד מ'ציוני הסטייה'. 

3. חלוקה במכפלת סטיות התקן של X ו-Y כפול גודל המדגם.

שאלה לדוגמא מתאם פירסון

חוקר פסיכולוג מעוניין לבדוק את הקשר בין עוצמת הפעילות הגופנית והתפקוד הקוגניטיבי בקרב מבוגרים. החוקר אסף נתונים מקבוצה של מבוגרים שהיו חלק ממחקר בריאות ארוך טווח. עוצמת הפעילות הגופנית נמדדה לפי מספר השעות שהנבדקים ביצעו פעילות גופנית בשבוע. כמו כן, תפקוד קוגניטיבי הוערך באמצעות מבחן שציוניו נעים בין 0 ל-100, כאשר ציונים גבוהים יותר מצביעים על תפקוד קוגניטיבי טוב יותר. החוקר משער כי יימצא מתאם חיובי בין עוצמת הפעילות הגופנית וציוני התפקוד הקוגניטיבי. 

הנח שנתוני המדגם מהטבלה מטה מתפלגים נורמלית באוכלוסייה וחשב את הקשר בין מספר שעות הפעילות גופנית בשבוע לבין ציוני התפקוד הקוגניטיבי.

 

פתרון:

בשאלה ניתן לראות שהמשתנים נמדדים בסולם רווח (ציון קוגניטיבי) ומנה/יחס (שעות פעילות). כמו כן, נתון לנו בשאלה שהמשתנים מתפלגים נורמלית באוכלוסייה. שתי פיסות מידע אלו, מעידים לנו שעלינו להשתמש במתאם פירסון על מנת לחשב את הקשר ביניהם.  בואו נסתכל על הנוסחה, נראה מה היא דורשת מאיתנו ואז נעקוב אחרי שלושת הצעדים לחישוב:


הנוסחה כוללת את הממוצע של משתנה X, הממוצע של משתנה Y , סטיות התקן של המשתנים וחישוב הסטיות של כל זוג תצפיות של המשתנים האלו. אז בואו ניגש לחישוב כל אחד מהמדדים הדרושים: 

ממוצעים:


 סטיות תקן:


חישוב ציוני סטייה:

כעת, לאחר שחישבנו את כל אחד מהמדדים, ניתן לבצע את צעדים 1 ו2 ע"י כך שנוסיף לכל משתנה עמודה המציינת את הסטייה של כל תצפית מהממוצע של המשתנה שלה, ולאחר מכן הכפלה בין שני ציוני הסטיות הללו: 

 

כעת, לאחר שיש לנו את המכפלה של ציוני הסטיות, ניתן לבצע את צעד 3 על ידי סכימה של כל מכפלת ציוני הסטיות וחלוקה במכפלת סטיות התקן וגודל המדגם:

 

פרשנות הממצאים

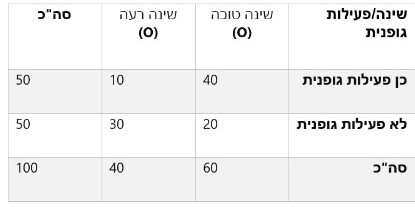
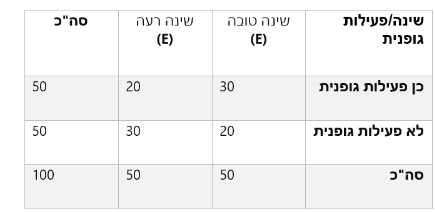
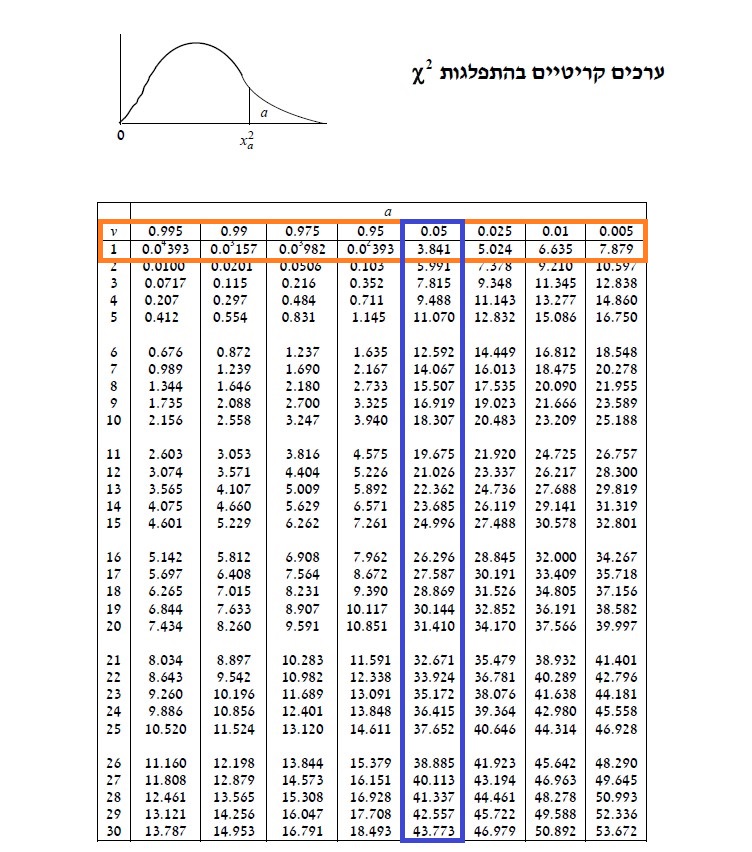
כמו שראינו, המתאם בין עוצמת הפעילות הגופנית לבין תפקוד קוגניטיבי הוא חיובי וחלש (מתחת ל-0.3). משמעות הדבר היא שככל שנתאמן יותר, כך התפקוד הקוגניטיבי שלנו ישתפר (ולהפך), אך בעוצמה חלשה יחסית.

סיכום

לסיכום, במאמר זה עברנו על מקדמי המתאם ועל החשיבות שלהם. למדנו על מבחן חי בריבוע כדי לבחון קיומו של קשר בין שני משתנים קטגוריאליים/שמיים והתקדמנו משם ל-V של Cramer הנועד להערכת עוצמת הקשר הזה. משם, עברנו אל מתאם ספירמן המודד קשרים מונוטוניים בין משתנים אורדינליים, ראינו כיצד מדרגים את התצפיות ומחשבים את המתאם ביניהם. לאחר מכן למדנו על מקדם המתאם של פירסון המודד קשרים לינאריים בין משתנים רציפים. באמצעות ייצוגים גרפיים,  הבנו כיצד ניתן לבחון את כיוון ועוצמת הקשרים המתאמים של ספירמן ופירסון. ראינו דוגמאות מעשיות ושיטות לחישוב כל מקדם מתאם ולמדנו כיצד ניתן להבין מתוך השאלה מהו המדד המתאים ביותר לשימוש. בטבלה מטה, תוכלו לראות סיכום של המדדים שעברנו עליהם ואת רמות המדידה המתאימות שלהם. להבנה מעמיקה יותר על סוגי מתאמים, קשרים וחישוב שלהם, מוזמנים להצטרף לקורס סטטיסטיקה שלנו.