בסטטיסטיקה, ערך הפי (p-value) הוא מדד שעוזר לנו לקבוע את הסבירות לקבל תוצאה מסויימת אם השערת האפס נכונה. השערת האפס היא הצהרה שמניחה כי לא קיים שום הבדל או קשר בין המשתנים הקיימים. p value הוא כלי חיוני המשמש אותנו בבדיקת השערות סטטיסטיות אשר באמצעותו ניתן להסיק מסקנות לגבי האוכלוסייה, על סמך ממצאי המדגם.
ערך ה-p מוגדר בתור הסיכוי לקבלת ערך קיצוני כמו, או קיצוני יותר, מהנתון שחושב במדגם, בהנחה שהשערת האפס נכונה. p-value מאפשר לנו לכמת את הראיות הדוחות את השערת האפס, בהתבסס על נתוני המדגם. באופן כללי, אם ערך ה-p קטן או שווה לרמת מובהקות [לינק פנימי לבדיקת השערות] קבועה מראש (בד"כ נקבעת ל0.05), משמעות הדבר הוא שבמידה והשערת האפס הנכונה (קרי, אין השפעה אמיתית באוכלוסייה של המשתנים), הסיכוי לקבל את תוצאת המדגם באופן מקרי הוא נמוך מספיק על מנת לקבל החלטה סבירה לדחות אותה. באותו האופן, אם ערך ה-p גדול מאלפא לא ניתן לומר שישנן ראיות מספיק חזקות לדחיית השערת האפס ולכן אנו מקבלים אותה.
חשוב לציין שערך ה – p לא מייצג את ההסתברות שהשערת האפס נכונה או לא. במקום זאת, ניתן להגדיר ערך זה בתור הסיכוי לקבלת התוצאה הנצפית, או תוצאה קיצונית ממנה, בהנחה שהשערת האפס נכונה. לכן, ערך p קטן לא אומר בהכרח שהשערת האפס שקרית, אלא שאילו השערת האפס הייתה נכונה, לא סביר שהתוצאה הנצפית התרחשה באופן מקרי.
ערך ה-p ממלא תפקיד מכריע בבדיקת השערות מכיוון שהוא עוזר לנו לקבוע את עוצמת הראיות נגד השערת האפס. זהו מדד למידת הסבירות לצפות בנתונים שיש לנו, בהנחה שהשערת האפס נכונה. כאשר ערך ה-p קטן, ניתן לומר שיש ראיות חזקות נגד השערת האפס, לכן נדחה אותה לטובת ההשערה החלופית (השערת החוקר). הנה כמה דוגמאות שיעזרו לנו להבין טוב יותר את השימוש בp value:
1. חברת תרופות בודקת תרופה חדשה לטיפול במצב רפואי מסוים. החוקרים עורכים ניסוי קליני עם קבוצת חולים המקבלת את התרופה וקבוצה נוספת המקבלת פלצבו. הם מודדים את ההבדל בתוצאות בין שתי הקבוצות ומחשבים ערך p של 0.03, מה שמצביע על כך שיש הבדל מובהק סטטיסטית בין שתי הקבוצות, וסביר להניח שההבדלים לא נובעים ממקריות בלבד.
2. מדען חברה עורך מחקר על הקשר בין הכנסה לאושר. הם סוקרים מדגם אקראי של 500 אנשים ומחשבים את מקדם המתאם בין הכנסה לאושר להיות 0.2 עם ערך p של 0.02. זה מצביע על כך שיש מתאם חיובי מובהק סטטיסטית בין הכנסה לאושר, כלומר אנשים עם הכנסה גבוהה יותר נוטים לדווח על רמות גבוהות יותר של אושר.
3. פסיכולוג עורך מחקר על יעילותו של טיפול חדש בדיכאון. הם מחלקים באופן אקראי את המשתתפים לקבל את הטיפול החדש או טיפול פלצבו ומודדים את השינוי בתסמיני הדיכאון שלהם לאורך זמן. הם מחשבים ערך p של 0.001, מה שמצביע על כך שיש הבדל מובהק סטטיסטית בין שתי הקבוצות וסביר שהטיפול החדש יהיה יעיל בטיפול בדיכאון.
בכל אחת מהדוגמאות הללו, ערך ה-p עוזר לחוקר לקבוע אם הממצאים שלהם מובהקים סטטיסטית או לא. בשאלות במבחנים לעתים מתייחסים לp value כאל "רמת המובהקות המינימלית". בואו נראה דוגמא לשאלה ופתרון מלא שלה:
פסיכולוג רוצה לחקור האם סוג חדש של טיפול יעיל בהפחתת רמות החרדה אצל מטופלים. רמת החרדה הממוצעת באוכלוסייה היא 50 עם סטיית תקן של 10. הפסיכולוג בוחר באקראי 25 מטופלים ומעניק להם את הטיפול החדש. לאחר הטיפול, הפסיכולוג רושם את רמות החרדה של מטופלים אלו ומחשב כי הממוצע הוא 46.5. מהי רמת המובהקות המינימלית שלגביה יוכל הפסיכולוג להסיק שהטיפול החדש יעיל בהפחתת רמות החרדה בקרב המטופלים?
פתרון:
כדי לפתור בעיה זו, נבצע בדיקת z של מדגם יחיד [לינק פנימי]. השערת האפס היא שהטיפול החדש אינו יעיל בהפחתת רמות החרדה אצל המטופלים, וההשערה האלטרנטיבית (השערת החוקר) היא שהטיפול החדש כן יעיל בהפחתת רמות החרדה בחולים. בשביל לפתור את השאלה, עלינו לעקוב אחר השלבים הבאים:
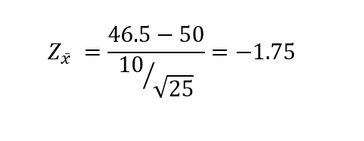
השערת האפס (הטיפול הנוכחי אינו יעיל בהפחתת רמות חרדה): H0: µ >= 50
השערת החוקר (הטיפול הנוכחי יעיל בהפחתת רמות חרדה): H1: µ < 50 (בדיקה חד-זנבית שמאלית)
כדי לבצע את מבחן ה-z, עלינו לחשב את הערך הסטטיסטי באמצעות הנוסחה הבאה:
כאשר x̄ הוא ממוצע המדגם, µ הוא ממוצע האוכלוסייה, σ הוא סטיית התקן של האוכלוסייה, ו-n הוא גודל המדגם. לאחר הצבת הנתונים, נקבל:
באמצעות טבלת התפלגות נורמלית [לינק פנימי] (טבלת זד), נוכל למצוא את השטח המצטבר של Z=1.75. אחד מינוס השטח שיימצא, ייתן לנו את השטח של הזנב הימני של ההתפלגות (כפי שניתן לראות בתרשים). מכיוון שההתפלגות הנורמלית היא סימטרית, השטח של הזנב הימני יהיה שווה לשטח של הזנב השמאלי וייתן לנו את ערך הp:
![]()
כלומר, עבור הנתונים הקיימים, רמת המובהקות המינימלית עבורה נדחה את השערת האפס היא 4.01% ומעלה. או במילים אחרות, אילו השערת האפס הייתה נכונה (קרי, הטיפול הנוכחי אינו יעיל בהפחתת רמות החרדה בקרב המטופלים), הסיכוי לקבל תוצאת מדגם כפי שנתקבלה או תוצאה קיצונית ממנה הוא 4.01%.
תרשים התפלגות נורמלית זנב ימני:
תרשים התפלגות נורמלית זנב שמאלי:
ערך p הוא ההסתברות לקבלת תוצאת מדגם כפי שנתקבלה או תוצאה קיצונית ממנה, בהנחה שהשערת האפס נכונה. אם ערך הp קטן מרמת המובהקות, אנו דוחים את השערת האפס. במילים אחרות, ערך הp הוא רמת המובהקות הקטנה ביותר שבעזרתה אנו יכולים לדחות את השערת האפס. ערך p ורמת המובהקות הם שניהם מדדים המשמשים כדי לקבוע האם על החוקר לדחות את השערת האפס בניתוח סטטיסטי. בעוד שרמת המובהקות מייצגת את ההסתברות המקסימלית לביצוע שגיאה מסוג I,p-value מייצג את ההסתברות לקבל את התוצאות הנצפות או תוצאות קיצוניות יותר במקרה, בהנחה שהשערת האפס נכונה. כאשר אתם נשאלים לגבי רמת המובהקות המינימלית, אתם בעצם נשאלים לגבי הסף התחתון שהחוקר מוכן לדחות את השערת האפס, שזהו למעשה ערך ה p.
לסיכום, ערך ה – p הוא מדד סטטיסטי המשמש לכימות הראיות הדוחות את השערת האפס. זהו כלי שימושי לקבלת החלטות בבדיקת השערות ורווחי סמך. על ידי הבנת המשמעות של ערך ה-p, תוכלו לקבל החלטות מושכלות יותר על סמך הנתונים הזמינים.