במאמר הבא נלמד על ביצוע בדיקת השערות ורווח סמך באמצעות מבחני t. בסיום המאמר, אתם תדעו כל מה שצריך לדעת על מבחני t, כולל מתי להשתמש בהם, איך הם שונים ממבחני z, ועוד.
מבחני t הם מבחנים סטטיסטיים שמשמשים להשוואת שני ממוצעי מדגם או השוואה של ממוצע מדגם בודד לממוצע האוכלוסייה. מבחנים אלו נמצאים בשימוש נרחב במחקרים ומשתמשים בהם לרוב על מנת לקבוע האם קיים הבדל מובהק בין שתי קבוצות.
מבחני t נקראים על שם התפלגות t, המשמשת לחישוב ההסתברות לקבלת ערך t מסוים. אנו נשתמש בהתפלגות t כאשר סטיית התקן של האוכלוסייה, סיגמה, אינה ידועה לנו. התפלגות t דומה מאוד בצורתה להתפלגות הנורמלית שאנחנו מכירים, אבל יש לה זנבות מעט "עבים" יותר. זאת אומרת, בהתפלגות t ישנם יותר ערכים קיצוניים מכיוון שהיא מבוססת על מדגם קטן יותר, מה שהופך אותה לפחות מדויקת. בתמונה למטה, תוכלו לראות את ההבדל בין התפלגות Z להתפלגות t בדרגות חופש (n-1) וגדלי מדגמים שונים:
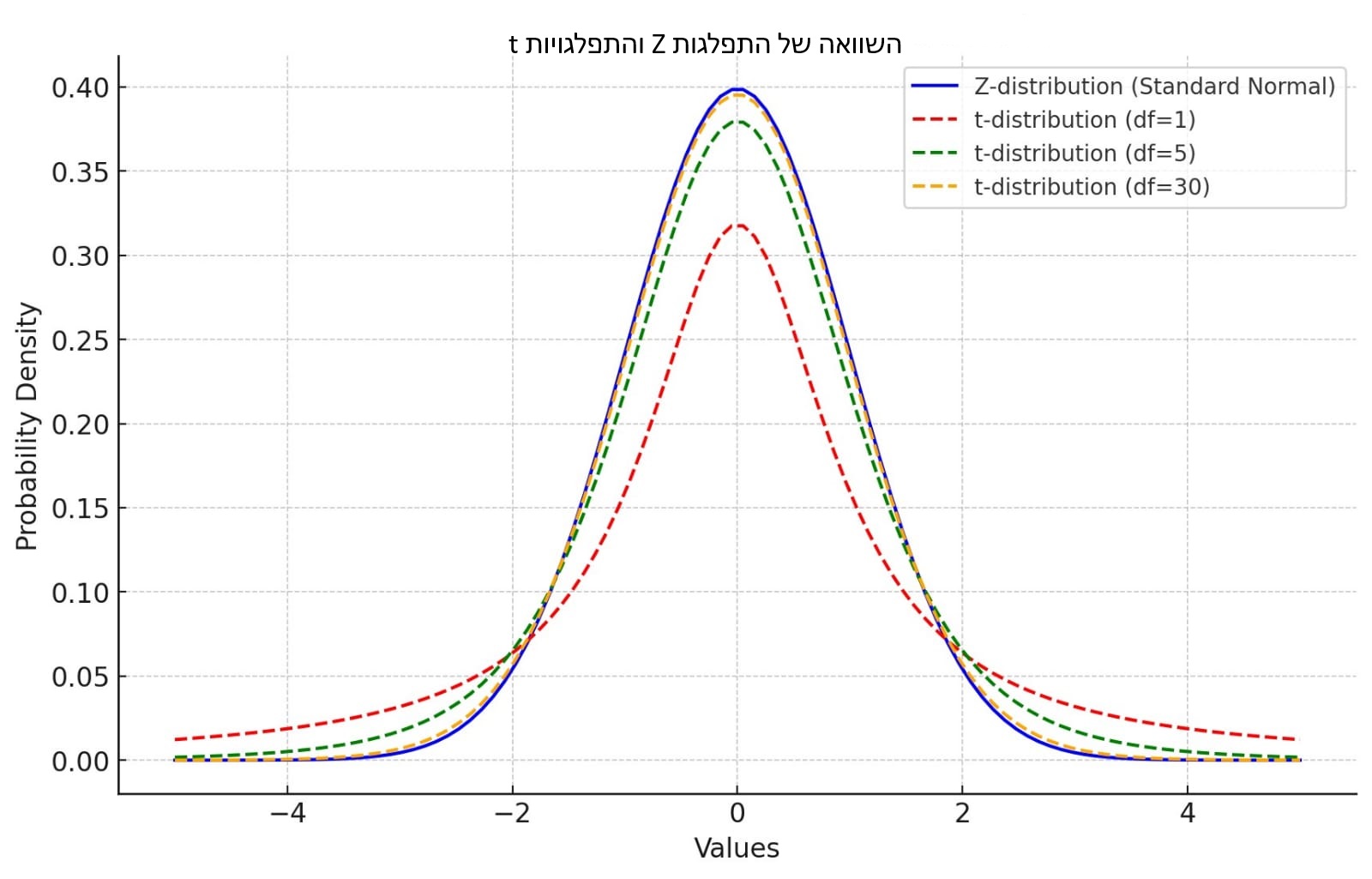כמו שאתם רואים, ככל שדרגות החופש (אשר מושפעות מגודל המדגם) הולכות ועולות, כך התפלגות t הולכת ודומה בצורתה להתפלגות Z. למעשה, אפשר להסתכל על התפלגות Z כעל התפלגות t עם אינסוף דרגות חופש (גודל מדגם של אוכלוסייה).
לפני שנתחיל להבין לעומק את מבחני ה-t , חשוב להבין שישנן מספר הנחות או תנאים שעלינו לעמוד בהן בעת שימוש במבחנים הללו.
הנחה ראשונה: הנחה ראשונה היא התפלגות נורמלית של הנתונים באוכלוסייה. כלומר על הנתונים באוכ' להתפלג נורמלית.
הנחה שנייה: במידה ואנו בודקים הבדלים בין שתי קבוצות, אזי התצפיות בין שתי הקבוצות יהיו בלתי תלויות אחת בשנייה או קשורות זו לזו.
הנחה שלישית: דגימה מקרית של התצפיות מתוך האוכלוסייה. כלומר על החוקר לדגום באופן מקרי ובלתי מוטה את התצפיות מתוך האוכלוסייה.
הנחה רביעית: במידה ואנו בודקים הבדלים בין שתי קבוצות, אז על שונויות שתי הקבוצות באוכלוסייה להיות שוות.
אבל מה קורה אם לא ידוע לנו כיצד מתפלגת האוכלוסייה, נורמלית או לא? או יותר גרוע מכך, אנחנו יודעים שהיא לא מתפלגת נורמלית? כאן נחלץ לעזרתנו משפט הגבול המרכזי אותו למדנו כבר:
משפט הגבול המרכזי רלוונטי במיוחד במבחני t מכיוון שהוא קובע שהתפלגות הדגימה של ממוצע המדגם תהיה נורמלית, ללא קשר לצורת התפלגות האוכלוסייה המקורית, במידה וגודל המדגם עולה על 30. המשמעות היא שאם ניקח מדגם גדול מספיק, התפלגות הדגימה של הממוצע תהיה נורמלית בקירוב, מה שיאפשר לנו להשתמש במבחני t בלי קשר לצורת התפלגות הנתונים באוכלוסייה.
מבחני t מתחלקים ל3 סוגים: מבחן t למדגם בודד, מבחן t למדגמים בלתי תלויים ומבחן t למדגמים תלויים או מזווגים ונעבור כעת על כל אחד מהם.
במבחני t למדגם בודד, אנו משווים ממוצע מדגם יחיד לממוצע ידוע של האוכלוסייה ובודקים באמצעות מבחן לבדיקת השערות האם הפער ביניהם הוא מובהק.
חישוב טעות התקן
בשאלות קודמות, תמיד סטיית התקן של האוכלוסייה, סיגמה, הייתה נתונה לנו והשתמשנו בה על מנת לחשב את סטיית התקן של התפלגות הדגימה, או במילים אחרות – את טעות התקן. אבל בפועל, המצב במציאות הוא מאוד שונה: סטיית התקן של האוכלוסייה כמעט אף פעם לא ידועה לנו. ולכן על מנת שנוכל לחשב את טעות התקן, אנו נשתמש בנתוני המדגם כדי לאמוד או להעריך את השונות של האוכלוסייה. במבחן t למדגם בודד שבו אנו משווים את ממוצע המדגם לממוצע ידוע באוכלוסייה, אנו נשתמש בנוסחה הזאתי:
ניתן לראות שהנוסחה מאוד דומה לנוסחה שאנו מכירים ולמדנו בסטטיסטיקה א' לחישוב השונות עם הבדל אחד קטן במכנה. מכיוון שאנחנו אומדים את השונות של האוכ' ולא משתמשים בשונות האמיתית, אנחנו למעשה מחלקים בn-1 ולא בn, שזה למעשה דרגות החופש. דרגות חופש מתייחסות למספר הערכים שיכולים או חופשיים להשתנות. תחשבו למשל על קבוצת אנשים שמנסה לבחור מאיזה מקום להזמין פיצה. אם קיימות N מסעדות, וכולם חופשיים לבחור איזו מסעדה שהם רוצים, אז ישנן N דרגות חופש. עם זאת, במידה ואדם אחד כבר החליט על מסעדת מסוימת, אז ישנן כעת רק N-1 דרגות של חופש . לאחר שנחשב את האומד לסטיית התקן של האוכלוסייה באמצעות שימוש בנתוני המדגם, אנו נציב בנוסחה לחישוב ציון התקן הסטטיסטי של t:
את הערך הסטטיסטי אנחנו נשווה לערך קריטי מטבלת t. הטבלה הבאה לקוחה מדף הנוסחאות של האוניברסיטה הפתוחה, אך של רוב המוסדות הטבלה דיי דומה והעיקרון זהה:
בחלק העליון (באדום) אנו נסתכל על רמת המובהקות שנדרשנו אליה בשאלה (בד"כ 5%). ובחלק השמאלי (בכחול), נסתכל על דרגות החופש המתאימות (n-1). כאשר נצליב את המידע משני המקומות הללו, אנחנו נקבל את הערך הקריטי המתאים. למשל, ברמת מובהקות של 5% עבור מדגם של 20 אנשים, אנחנו נסתכל על אלפא שווה 0.05 ו19 דרגות חופש, ונראה שהערך הקריטי המתאים הוא 1.746:
כמו במבחן זד, גם כאן יש לנו השערות חד-זנביות והשערות דו זנביות. גם כאן ההשערה החד זנבית מתחלקת להשערה חד זנבית ימנית, והשערה חד זנבית שמאלית. השערה עם זנב שמאלי קובעת שממוצע המדגם נמוך משמעותית מ-ממוצע האוכלוסייה, וסט ההשערות ייכתב כך:
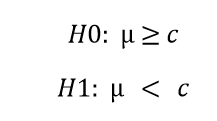
* כאשר C יהיה ערך הפרמטר לפי השערת האפס.
בהשערה עם זנב שמאלי, כאשר סטטיסטי המבחן יהיה קטן יותר מהערך הקריטי, אנו נמקם אותו באזור הדחייה ונדחה את השערת האפס.
השערה ימנית, לעומת זאת, קובעת שממוצע המדגם יהיה גבוה משמעותית מ-ממוצע האוכלוסייה ועל כן סט ההשערות יראה כך:
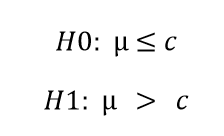
בהשערה עם זנב ימני, כאשר סטטיסטי המבחן יהיה גדול יותר מהערך הקריטי, הוא ימוקם באזור הדחייה ונדחה את השערת האפס.
השערה דו-זנבית אינה מתחייבת לגבי כיוון ספציפי בנוגע לממוצע המדגם בהשוואה לממוצע האוכלוסייה. במקום זאת, בהשערה דו זנבית, החוקר בודק האם ממוצע המדגם שונה באופן מובהק מ-ממוצע האוכלוסייה בכל כיוון שהוא. וסט ההשערות ייראה כך:
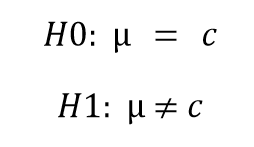
בהשערה דו זנבית אנחנו נחצה את רמת המובהקות, מה שיקשה על החוקר לדחות את השערת האפס. בהשערה דו זנבית, כאשר ערך סטטיסטי המבחן t יהיה גדול מהערך הקריטי העליון או קטן מהערך הקריטי התחתון , אנו נמקם אותו באחד מאזורי הדחייה ונדחה את השערת האפס. מאחר והשערה זו אינה "מתחייבת" לאף כיוון, כמו בפעמים קודמות, אנו נחצה את רמת המובהקות עבור כל אחד מאזורי הדחייה.
דוגמא
בואו נראה דוגמא לשאלה של מבחן t למדגם בודד:
חברה רוצה לבדוק האם הזמן הממוצע שלוקח לשירות הלקוחות שלה להגיב לפנייה גדול משמעותית מ-3 דקות. לצורך כך נלקח מדגם אקראי של 10 פניות ונרשמו זמני התגובה הבאים (בדקות):
4.5, 3.2, 5.1, 4.9, 3.8, 4.1, 5.5, 4.2, 5.2, 4.8
בדוק את ההשערה שזמן המענה הממוצע גדול מ-3 דקות ברמת מובהקות של 0.05 באמצעות המבחן הסטטיסטי המתאים.
בכדי לבדוק את ההשערה, עלינו לערוך מבחן t למדגם בודד. על מנת לפתור את השאלה, בואו נעבור על השלבים הבאים:
השערת האפס (H0): זמן המענה הממוצע אינו גדול מ-3 דקות. או במונחים סטטיסטיים µ=3
השערת החוקר (H1): זמן המענה הממוצע גדול מ-3 דקות. או µ > 3
רמת המובהקות הנתונה בשאלה היא 0.05
חישוב האומדן לסטיית התקן של האוכלוסייה, S כובע:
נחשב באמצעות הצבה בנוסחה הבאה:
הצבה:
על מנת לקבוע אזורי דחייה וקבלה, עלינו למצוא ראשית את הערך הקריטי בטבלת t לפי 9 ד"ח (בכחול) ורמת מובהקות של 0.05 (באדום), הערך הקריטי הוא 1.833 (בסגול). מכאן אנו מבינים שהערך הסטטיסטי גדול מהערך הקריטי ולכן ימוקם באזור הדחייה של השערת האפס:
בסוף הפתרון, לאחר שכתבנו את כל החישובים, אנו נכתוב את המסקנה שלנו: מכיוון שהערך הסטטיסטי גדול מהערך הקריטי , הוא ימוקם באזור הדחייה של השערת האפס. לפיכך, ברמת מובהקות של 5%, נוכל לדחות את השערת האפס ולהסיק שזמן המענה הממוצע באוכלוסייה גדול באופן מובהק מ-3 דקות.
מבחני t למדגמים בלתי תלויים משמשים להשוואה בין ממוצעים של שתי קבוצות נפרדות. דוגמה לכך יכולה להיות הערכת היעילות של התערבות טיפולית על ידי השוואת ממוצע רמות הדיכאון של קבוצה שמקבלת טיפול לאלו של קבוצת ביקורת שאינה מקבלת את הטיפול. כאן, שתי הקבוצות אינן תלויות זו בזו, כלומר המשתתפים בקבוצה אחת אינם משפיעים או אינם חלק מהקבוצה השנייה.
לעומת זאת, מבחני t תלויים או מזווגים, משמשים להשוואת הממוצעים בתוך אותה קבוצה בזמנים שונים או בתנאים שונים. לדוגמה, מדידת משקל לפני ואחרי התחלה של דיאטה מסוימת. במקרים של מבחן t למדגמים מזווגים, אותם אנשים מוערכים פעמיים, מה שהופך את הציונים שלהם לפני ואחרי הסדנה תלויים.
ההבדל העיקרי בין שני סוגי המבחנים הללו טמון ביחסים בין הקבוצות המושוות. מבחני t בלתי תלויים מנתחים את ההבדלים בין שתי קבוצות נפרדות, ואילו מבחני t תלויים בוחנים את ההבדלים בתוך אותה קבוצה על פני שני תנאים או נקודות זמן. הבחנה זו חיונית לבחירת המבחן הסטטיסטי המתאים ולפענוח מדויק של התוצאות.
בואו נראה דוגמא לשאלה על מנת שדברים יהיו ברורים יותר:
חברה רוצה לבדוק האם הדיוק של מודל הבינה המלאכותית שלה לסיווג תמונה שונה משמעותית בין שתי שיטות אימון. החברה בחרה באקראי 15 תמונות ורשמה את ציון הדיוק (מתוך 100) עבור כל תמונה בכל שיטת אימון. הנתונים הם כדלקמן:
שיטת אימון א':
78, 80, 85, 75, 70, 82, 72, 84, 76, 88, 79, 83, 81, 77, 74
שיטת אימון ב':
88, 92, 90, 85, 82, 87, 91, 85, 89, 93, 86, 84, 87, 91, 84
בדוק את ההשערה שציון הדיוק הממוצע של מודל הבינה המלאכותית שונה משמעותית בין שתי שיטות האימון ברמת מובהקות של 0.05 באמצעות המבחן הסטטיסטי המתאים.
מילות מפתח:
ראשית, על מנת להבין שמדובר במבחן t למדגמים בלתי תלויים, אנו נסתכל על מילות המפתח "שני מדגמים שונים". הדבר מצביע לנו על כך שאנו עוסקים בדגימות בלתי תלויות. במילים אחרות, כל תצפית במדגם אחד בלתי תלויה או קשורה למדגם השני ועל כן עלינו לבצע מבחן t למדגמים בלתי תלויים.
כדי לבחון את ההשערה שציון הדיוק הממוצע של מודל הבינה המלאכותית שונה באופן משמעותי בין שתי שיטות האימון שונות, עלינו לבצע מבחן t למדגמים בלתי תלויים.
השערת אפס (Ho): ציון הדיוק הממוצע של מודל הבינה המלאכותית זהה בין שתי שיטות אימון שונות.
µ1-µ2=0
השערת החוקר (H1): ציון הדיוק הממוצע של מודל הבינה המלאכותית שונה באופן משמעותי בין שתי שיטות אימון שונות.
µ1-µ2≠0
נחשב את ממוצעי המדגם ואת האומדן לסטיות התקן עבור כל שיטת אימון.
עבור שיטת אימון א':
ממוצע מדגם:
אומדן לשונות המדגם:
עבור שיטת אימון ב':
ממוצע מדגם:
אומדן לשונות המדגם:
כעת נוכל לחשב את השונות המשותפת של שני המדגמים יחד באמצעות שימוש בנוסחה הבאה:
נציב:
כעת נוכל לחשב את ה-t סטטיסטי :
כאשר n1 ו-n2 הם גדלי המדגם עבור כל שיטת אימון. ובמכנה אנחנו מציבים את השונות שחישבנו עבור כל מדגם.
נציב:
באמצעות טבלת התפלגות t עם 28 דרגות חופש (n1 + n2 – 2) ברמת מובהקות של 0.05 דו זנבית (שזה שווה ערך לרמת מובהקות 0.025 חד זנבית), אנו נראה שערך t הקריטי הוא ±2.048:
מכיוון שערך ה-t המחושב נמצא מחוץ לטווח ערכי ה-t הקריטיים, אנו נמקם את הערך הt הסטטיסטי באזור הדחייה ונדחה את השערת האפס. כלומר ברמת מובהקות 0.05, אנו נסיק כי ציון הדיוק אכן שונה באופן משמעותי בין שתי שיטות אימון שונות.
כמו במבחני זד, גם באמצעות מבחני t אנחנו יכולים לבצע רווח סמך. המטרה של רווחי הסמך באמצעות שימוש במבחני t היא זהה למטרה של מבחני זד: אמידת הפרמטר באוכלוסייה. אולם, ישנו הבדל אחד קריטי – סטיית התקן של האוכלוסייה אינה ידועה ולכן עלינו לאמוד אותה.
כאשר אנו מבצעים רווח סמך באמצעות מדגם בודד, המטרה היא לאמוד את תוחלת האוכלוסייה. אולם, כאשר אנו משתמשים בשני מדגמים (תלויים או בלתי תלויים), המטרה היא לאמוד את הפרש התוחלות באוכלוסייה. כמו בבדיקת השערות, כאשר ברצוננו לאמוד את הפרמטר באוכלוסייה וסטיית התקן אינה ידועה לנו, אנו נאמוד אותה ואז נשתמש בערך הקריטי מטבלת t עבור רווח הסמך.
כאשר נרצה לבצע רווח סמך באמצעות t למדגם בודד, אנו נשתמש בנוסחה הבאה:
שימו לב שגם כאן כמו ברווח סמך עם טבלת זד, אנחנו חוצים את האלפא. כמו כן, בסוגריים מעל ערך הt, מצוינות דרגות החופש.
בואו נראה דוגמא לשאלה על מנת שדברים יהיו ברורים יותר:
משך זמן הנסיעה של אדם הרגיל לנסוע לעבודתו בשעה קבועה בבוקר מתפלג נורמלית עם ממוצע 24 דקות. כאשר נפתחה דרך חדשה בכיוון נסיעתו, הוא רצה לאמוד את זמן הנסיעה בדרך החדשה.
לצורך כך הוא נסע בדרך החדשה ב- 12 ימים מקריים, ומשכי זמן הנסיעה (בדקות) היו כך:
.23 ,25 ,11 ,27 ,19 ,24 ,21 ,23 ,18 ,33 ,21 ,19
ברמת ביטחון 95%, אמוד את תוחלת זמן הנסיעה באמצעות הדרך החדשה.
ראשית כל, בואו נבין מהן מילות המפתח שנמצאות בשאלה שעזרו לנו להבין שמדובר ברווח סמך t למדגם בודד:
1. התפלגות נורמלית: כתוב לנו שהמשתנה באוכלוסייה (זמן הנסיעה) מתפלג נורמלית.
2. אמידה ורמת ביטחון: כתוב שעלינו לאמוד ברמת ביטחון של 95%, מכאן אנו מבינים שרוצים שנשתמש ברווח סמך כלשהו.
3. כמות המדגמים: בנוסף , נלקח מדגם אחד בלבד ועל כן מדובר ברווח סמך למדגם בודד.
4. אמידת סטיית התקן: סטיית התקן באוכלוסייה אינה ידועה או נתונה לנו בשאלה ולכן עלינו לאמוד אותה ולהשתמש במבחן t.
מארבעת אלו, אנו יכולים להבין שמבקשים מאיתנו בשאלה להשתמש בנוסחת הרווח סמך. כעת בואו נראה את הפתרון
ממוצע המדגם:
אומדן לסטיית התקן:
רמת הביטחון הנתונה בשאלה , אחד מינוס אלפא, שווה 95% ולכן רמת המובהקות (המשלימה ל100%, אלפא) היא 5%. מכיוון שמדובר ברווח סמך, אנו חוצים את האלפא ומתייחסים לזנב של 2.5% לכל צד. לכן, בטבלת t נצליב את העמודה של אלפא שווה 2.5% או 0.025 עם השורה של דרגות החופש המתאימות , 11 (12 פחות אחת) ונקבל שערך הt הקריטי הוא פלוס מינוס 2.201 או בכתיב סטטיסטי:
טבלת t:
כעת על שעלינו לעשות הוא להציב בנוסחת הרווח סמך:
בחישוב מהיר נראה שהתוצאה היא שממוצע זמן הנסיעה באמצעות הדרך החדשה באוכלוסייה, ברמת ביטחון של תשעים וחמישה אחוזים נע בין 18.58 ל25.41. במונחים סטטיסטיים נכתוב זאת כך:
כעת זהו השלב שאנו לוקחים את הממצאים שקיבלנו, ונותנים להם פרשנות מילולית. ראינו שתוחלת זמן הנסיעה נע בין 18.58 ל25.41. לכן התשובה תהיה שברמת ביטחון של 95% ניתן לומר שתוחלת זמן הנסיעה יהיה בין 18.58 ל25.41 דקות.
כעת נעבור לחישוב רווח סמך באמצעות שימוש במבחן t למדגמים בלתי תלויים. כאשר נרצה לעשות זאת, נצטרך לעשות שימוש בנוסחה הבאה:
שימו לב שגם כאן נצטרך לחשב את האומדן לסטיית התקן של האוכלוסייה באמצעות אחת משתי הנוסחאות הבאות:
שני מפעלים המייצרים גאדג'טים מעוניינים להשוות את המשקל הממוצע של הגאדג'טים המיוצרים על ידי כל מפעל. הם לוקחים מדגם אקראי של 10 גאדג'טים ממפעל A ומוצאים שהמשקל שלהם הוא:
10, 12, 14, 11, 13, 12, 14, 11, 13 ו-15 גרם.
לאחר מכן, נלקח מדגם אקראי של 12 גאדג'טים ממפעל B ומוצאים שהמשקל שלהם הוא:
9, 11, 10, 12, 11, 13, 14, 12, 10, 11, 13 ו-14 גרם.
אמוד ברמת ביטחון 99% את הפרש במשקל הממוצע באוכלוסייה של גאדג'טים המיוצרים על ידי מפעל A ומפעל B
מילות מפתח
ראשית כל, בואו נבין מהן מילות המפתח שנמצאות בשאלה שעזרו לנו להבין שמדובר ברווח סמך t לשני מדגמים בלתי תלויים:
1. השוואה בין שני מדגמים: אנו רואים שמדובר בהשוואה בין שני מדגמים (מפעל A ומפעל B) ולכן אנו יכולים להשתמש במבחן t למדגמים תלויים או בלתי תלויים.
2. תלות/אי תלות: מכיוון שמדובר בשני מפעלים נפרדים, ניתן להבין שמדובר במדגמים לא קשורים ולכן עלינו לבחור במבחן t למדגמים בלתי תלויים.
3. אמידה ורמת בטחון: לבסוף, מכיוון שנתבקשנו לאמוד ברמת ביטחון מסוימת את הפרמטר באוכלוסייה, אנו יכולים להבין שמדובר ברווח סמך.
שלוש אלו מאפשרים לנו להבין שעלינו לעשות שימוש ברווח סמך של מבחני t למדגמים בלתי תלויים. בואו נראה את הפתרון בצעדים.
עבור מפעל A:
ממוצע המדגם:
אומדן לסטיית תקן:
עבור מפעל B:
ממוצע המדגם:
אומדן לסטיית תקן:
לאחר מכן, נחשב את סטיית התקן המשותפת על ידי הצבת סטיית התקן של כל מדגם בנוסחה:
כעת, לאחר שחישבנו הנתונים המדגמיים (ממוצעים וסטיות תקן), אפשר להתפנות לחיפוש הערך הקריטי בטבלת t. נתון בשאלה שרמת הביטחון (1–α) היא 99% ולכן אנו מבינים שרמת המובהקות (α) היא 1%. מכיוון שברווח סמך אנו מחלקים את האלפא לכל אחד מהזנבות של ההתפלגות, אנו נחפש את הערך הקריטי שתואם לרמת מובהקות של חצי אלפא או במקרה הנוכחי, חצי אחוז (0.005/0.5%). כמו כן, נסתכל על 20 דרגות חופש (10+12-2) ונמצא את הערך הקריטי ±2.845:
כעת כל שעלינו לעשות הוא להציב בנוסחת הרווח סמך:
לאחר חישוב נקבל:
כעת זהו השלב שאנו לוקחים את הממצאים שקיבלנו, ונותנים להם פרשנות מילולית. ראינו שהפרש תוחלות משקל הגאדג'טים נע בין 0.69- ל2.37 גרם. לכן התשובה תהיה שברמת ביטחון של 99% ניתן לומר שהפרש תוחלות המשקל יהיה בין 0.69- ל2.37 גרם.
כאשר נרצה להשתמש במבחן t למדגמים תלויים לצורך חישוב רווח סמך, נעשה שימוש בנוסחה הבאה:
רווח סמך במבחן t למדגמים מזווגים מייצג את הטווח שבו אנו חושבים שההפרש הממוצע האמיתי בין שתי קבוצות של מדידות עשוי להימצא בו. למשל, רווח סמך של 95% נותן טווח של ערכים שבו אנו בטוחים ב-95% שההפרש הממוצע האמיתי נופל בטווח הזה.
חדר כושר מעוניין להעריך את האפקטיביות של תוכנית אימונים חדשה על כמות המשקל שהם מרימים בדחיקת חזה. חדר הכושר בחר מדגם אקראי של 10 חברים ומודד את כוחם לפני ואחרי תוכנית האימון ואלו התוצאות (בק"ג):
אמוד ברמת בטחון 95% את ההבדל בעליית המשקל הממוצעת לפני ואחרי תוכנית האימון.
לפני הפתרון בשלבים, הבה נבין מה בשאלה הצביע על כך שעלינו להשתמש ברווח סמך לt עבור מדגמים תלויים:
1. שני מדגמים: בשאלה ניתן לראות שישנה שיטה אחת שנמדדה על שני מדגמים ועל כן עלינו להשתמש במבחן t לשני מדגמים (תלויים או בלתי תלויים).
2. מדידה "לפני ואחרי": ניתן לראות שמדידת הכוח של המתאמנים מתבצע לפני יישום התוכנית ואחרי יישום התוכנית. מילות מפתח אלה, מעידות על כך שעלינו להשתמש במבחן t למדגמים תלויים.
3. אמידה ברמת ביטחון: בשאלה אנו מתבקשים לאמוד את ההבדל ברמת ביטחון מסוימת. השימוש במילים האלו: אמידה ורמת ביטחון, מצביע על כך שעלינו לבצע רווח סמך.
אם נחבר את שלוש אלו יחדיו, נבין שעלינו לבצע רווח סמך t למדגמים תלויים.
ראשית, עלינו לחשב את ההבדלים במשקל ההרמה לפני ואחרי תוכנית האימון עבור כל חבר. אם נארגן זאת מחדש בטבלה, זה ייראה כך:
מס' חבר | הרמה לפני (ק"ג) | הרמה אחרי (ק"ג) | הפרש |
1 | 100 | 110 | 10 |
2 | 95 | 102 | 7 |
3 | 85 | 92 | 7 |
4 | 110 | 115 | 5 |
5 | 90 | 96 | 6 |
6 | 102 | 108 | 6 |
7 | 97 | 103 | 6 |
8 | 80 | 85 | 5 |
9 | 115 | 118 | 3 |
10 | 100 | 106 | 6 |
לאחר מכן נחשב את הממוצע ואת סטיית התקן של ההפרשים:
ממוצע:
אומדן לסטיית תקן:
מאחר ורמת הביטחון היא 95%, רמת המובהקות שצריכה להשלים ל100%, תהיה 5%. לכן, באמצעות טבלת התפלגות t עם 9 דרגות חופש (n-1) ורמת מובהקות של 2.5% לכל צד, נוכל למצוא כעת את הערך הקריטי: ±2.262
כעת כל שעלינו לעשות הוא להציב בנוסחת הרווח סמך:
לאחר חישוב נקבל:
כעת זהו השלב שאנו לוקחים את הממצאים שקיבלנו, ונותנים להם פרשנות מילולית. שההפרש (השיפור) הממוצע באוכלוסייה לפני ואחרי יישום שיטת האימון ברמת ביטחון של 95% יהיה בין 4.81 ק"ג ל7.38 ק"ג.
לסיכום
לסיכום, מבחני t הינם כלי סטטיסטי הנועד להשוות הממוצעים של שתי קבוצות, או של קבוצה אחת לממוצע האוכלוסייה, כאשר שונות האוכלוסייה אינה ידועה.
במאמר הזה הבנו מתי וכיצד יש להשתמש במבחני t, מהן ההנחות הדרושות לשימוש במבחן זה וכיצד ניתן לזהות באיזה סוג של מבחן t עלינו להשתמש. למדנו גם על רווח סמך עבור מבחני t ואיך מפרשים את התוצאות שהתקבלו.
