בתחום העצום של הסטטיסטיקה, הרעיון של התפלגות דגימה מהווה את הבסיס להכל. בבסיסה, התפלגות הדגימה היא התפלגות של נתון מסוים הנגזר ממדגמים רבים בגודל נתון שנלקחו מתוך אוכלוסייה ספציפית. הסיבה שבגללה התפלגות הדגימה היא כה חיונית היא בשל יכולתה להציע תובנות לגבי השונות והדיוק של ההשערות הסטטיסטיות שלנו, ובכך לאפשר לנו לבצע בדיקת השערות בהקשרים מחקריים שונים.
כדי להבין באמת את מהות התפלגויות הדגימה, חיוני להבחין בינה לבין שתי התפלגויות יסוד אחרות: התפלגות האוכלוסייה והתפלגות המדגם. התפלגות האוכלוסייה מייצגת את כלל נקודות הנתונים באוכלוסייה, ומציגה את התדירות או השכיחות שבה כל ערך מתרחש. מצד שני, התפלגות המדגם מתייחסת להתפלגות נקודות הנתונים בתוך מדגם בודד ספציפי שנלקח מאוכלוסייה זו.
לעומת זאת, התפלגות הדגימה לוקחת צעד אחורה כדי להסתכל על התמונה הרחבה יותר. במקום להתמקד בנקודות נתונים בודדות, היא מתייחסת להתפלגות של נתון מדגם מסוים (כמו ממוצע או חציון) על פני מדגמים מרובים מהאוכלוסייה. על ידי הבנת התפלגות זו, ניתן להסיק מסקנות לגבי אוכלוסיות, אפילו כאשר אנו מצוידים רק בנתונים מחלק קטן מהם.
פרמטר מתייחס לערך מספרי המאפיין היבט של אוכלוסייה שלמה. למשל, אם היינו לוקחים בחשבון את הגבהים של כל אדם במדינה, הגובה הממוצע המחושב יהיה פרמטר האוכלוסייה. מצד שני, הסטטיסטי הוא ערך מספרי המתאר מאפיין של מדגם, שהוא רק תת-קבוצה של אותה האוכלוסייה. למשל, אם היינו מודדים את הגבהים של קבוצה אחת של פרטים מתוך מדינה מסוימת, הגובה הממוצע של קבוצה זו יהיה סטטיסטי המדגם.
היופי בסטטיסטיקה טמון בהבנה שלעתים קרובות איננו יכולים למדוד אוכלוסייה שלמה – זה לא מעשי או בלתי אפשרי. לכן, אנחנו לוקחים דגימות ומחשבים סטטיסטי, כמו ממוצע המדגם. האתגר אם כן הוא להסיק על הפרמטר של האוכלוסייה מתוך הנתון המדגמי הזה (הסטטיסטי), ומכאן מגיע הרעיון של התפלגות הדגימה. התפלגות הדגימה מספקת מסגרת שעוזרת לנו להבין כיצד ממוצע המדגם שלנו קשור לממוצע האוכלוסייה בפועל, וכמה שונות אנו יכולים לצפות בין ממוצעי המדגם השונים. הבנת הקשר הזה הוא המפתח להסקת מסקנות מדויקות ומשמעותיות לגבי האוכלוסייה הגדולה יותר בעזרת נתוני המדגם שלנו.
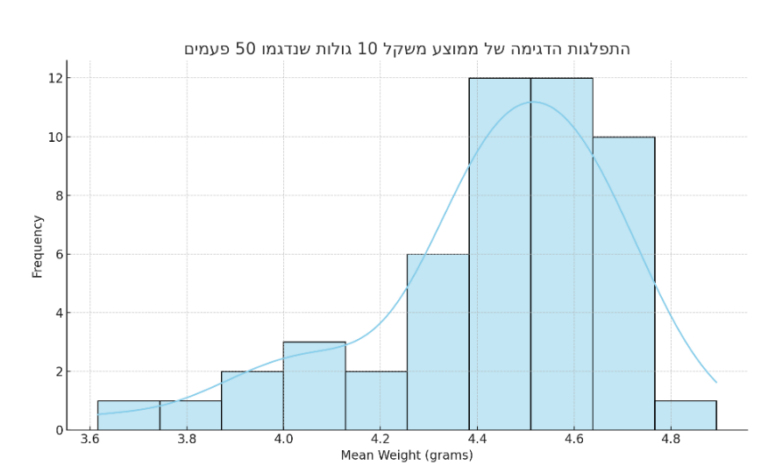
כדי להבין איך נוצרת התפלגות הדגימה, תארו לעצמכם שיש לכם כד עצום מלא באינספור גולות, שכל אחת מהן מייצגת נקודת נתונים בודדת באוכלוסייה. לאחר מכן, באופן אקראי אנחנו נדגום מספר קבוע מראש של גולות (נניח 10 גולות) מהכד. בואו נניח, עבור מקרה זה בלבד, שאת אותן 10 גולות דגמנו 50 פעמים. אחרי שעשינו את זה נחשב את הערך הסטטיסטי – המשקל הממוצע של הגולות שנבחרו. לאחר שמצאנו את הממוצע, אנו מחזירים את כל הגולות לתוך הכד, ובכך אנו מבטיחים שהאוכלוסייה תישאר ללא שינוי. לאחר מכן, נוציא עוד מדגם אקראי של 10 גולות ונחשב את הממוצע של המדגם החדש הזה. תיאורטית, היינו ממשיכים בתהליך הזה מספר אינסופי של פעמים, כאשר בכל פעם היינו מחשבים את הממוצע של המדגם ואז מחזירים את הגולות לכד, אבל לצורך הדוגמא נסתפק ב50 פעמים בלבד. ככל שנמשיך לרשום את הממוצעים מכל מדגם, לאורך זמן, אנו נראה שמתגלה דפוס. הממוצעים הללו יתחילו ליצור התפלגות משלהם – התפלגות הדגימה של הממוצע, כפי שניתן לראות באיור מטה:
דגימה אקראית: יש לדגום את הנתונים באופן אקראי מהאוכלוסייה. לכל תצפית בודדת צריך להיות סיכוי שווה להיכלל במדגם.
אי תלות: התצפיות במדגם חייבות להיות בלתי תלויות זו בזו. הדבר מתקיים לעתים קרובות אם גודל המדגם מהווה פחות מ-10% מגודל האוכלוסייה.
גודל המדגם: למרות שאין סף קפדני, כלל אצבע הוא שגודל המדגם צריך להיות לפחות 30 (n≥30). עבור אוכלוסיות שאינן מתפלגות באופן נורמלי באופן מובהק, ייתכן שיידרשו גדלי מדגם גדולים יותר כדי שהתפלגות הדגימה תתקרב לנורמליות.
היופי של משפט הגבול המרכזי טמון בהשלכות שלו על צורת התפלגות הדגימה. גם אם התפלגות האוכלוסייה המקורית הייתה מוטה, יש לה בולטות מסוימת או בעלת צורה שהיא רחוקה מעקומת הפעמון הקלאסית, התפלגות הדגימה של ממוצע המדגם תיטה להתפלגות נורמלית ככל שגודל המדגם יגדל. צורה נורמלית אופיינית זו, המכונה לעתים קרובות "עקומת הפעמון", היא סימטרית לגבי הממוצע ומתארת את הסבירות לקבל ממוצעי מדגם שונים. ככל שגודל המדגם גדול יותר, כך התפלגות זו תהיה קרובה יותר לעקומת פעמון מושלמת.
התפלגות הדגימה של ממוצע המדגם היא המוכרת ביותר, בעיקר בשל הקשר שלה עם משפט הגבול המרכזי. כפי שהדגשנו, לא משנה מהי צורת התפלגות האוכלוסייה, התפלגות הדגימה של הממוצע נוטה להתפלגות נורמלית ככל שגודל המדגם עולה. מאפיין זה מתקיים גם אם האוכלוסייה המקורית אינה מתפלגת נורמלי, מה שהופך אותה לכלי חזק להסקת מסקנות סטטיסטיות.
כאשר n זהו גודל המדגם וp זהו הפרופורציה (או שיעור ההצלחה) באוכלוסייה.
כמו כן, כפי שניתן לראות באיור מטה, גם מידת הסימטריות של שיעור ההצלחה באוכלוסייה, משפיע על צורת התפלגות הדגימה של הפרופורציה:
כפי שניתן לראות, ללא קשר לגודל המדגם, ככל שהפרופורציה של האוכלוסייה יותר קיצונית (אדום וסגול), צורת ההתפלגות נהיית פחות דומה לפעמון, בהשוואה למצבים בהם פרופורציית האוכלוסייה יותר נוטה לסימטריות (התפלגות כתומה, ירוקה וכחולה). ככל שגודל המדגם עולה, כך התפלגות הדגימה הופכת בצורתה לפעמונית יותר, ללא קשר להתפלגות האוכלוסייה המקורית, הודות למשפט הגבול המרכזי. כמו כן, גודל מדגם גדול יותר מוביל גם לטעות תקן קטנה יותר, מה שמרמז על פחות שונות בין סטטיסטי מדגם שונים. לצורך המחשה, בואו נחזור לדוגמא של הגולות ממקודם, אך הפעם ניקח מדגם של 10 תצפיות 100,000 פעם ומדגם של 40 תצפיות 100,000 פעם ונראה מה קורה:
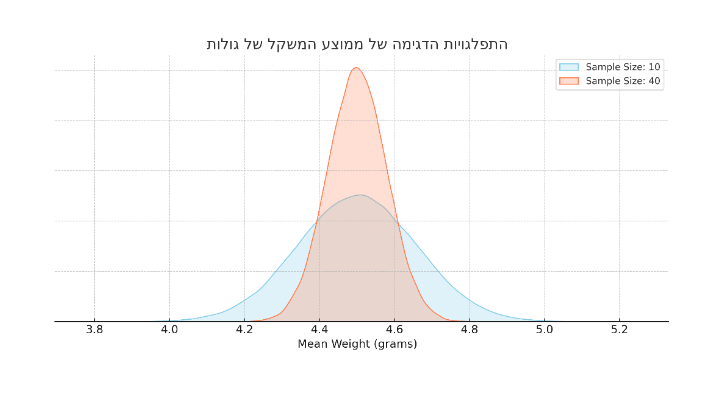
כמו שניתן לראות, התמונה מציגה את התפלגות הדגימה של משקלי גולות עבור שני גדלי דגימה: 10 ו-40 גולות שנדגמו 100,000 פעמים. האזור הכחול מציג את השונות במשקלים הממוצעים על פני מדגמים של 10 גולות. לעומת זאת, האזור האדום, מציג את המשקלים הממוצעים עבור דגימות גדולות יותר של 40 גולות. ניתן לראות שההתפלגות עבור גודל המדגם הגדול יותר מרוכזת יותר, ומשקפת שונות מופחתת בין ממוצעי המדגם.
הגודל היחסי בין המדגם לאוכלוסייה, בא לידי ביטוי גם הוא בעת דגימה ללא החזרה מאוכלוסיות סופיות. כאשר גודל המדגם מהווה חלק משמעותי מהאוכלוסייה (בדרך כלל יותר מ-5%), לגורם זה עשויה להיות השפעה רבה, ע"י צמצום התפשטות התפלגות הדגימה.
ככל שהשונות או הפיזור באוכלוסייה גדולה יותר, כך השונות בהתפלגות הדגימה גדולה יותר גם כן. הסיבה לכך היא שמדגמים שנלקחו מאוכלוסייה עם שונות גבוהה, נוטים יותר לייצר נתוני מדגם השונים באופן משמעותי מפרמטר האוכלוסייה. טעות התקן, המודדת את השונות של התפלגות הדגימה, עומדת ביחס ישר לסטיית התקן של האוכלוסייה.
במחקר רפואי, הבנת התפלגות הדגימה היא חיונית. למשל, בעת בדיקת יעילותה של תרופה חדשה, החוקרים יוכלו לנתח את התוצאות הממוצעות ממדגם של משתתפים. התפלגות הדגימה עוזרת לקבוע האם ההשפעות שנצפו הן מובהקות סטטיסטית או שהן היו יכולות להתרחש גם במקרה.
סוקרים אוספים נתונים מחלק מציבור הבוחרים כדי לחזות את תוצאות הבחירות. הבנת התפלגות הדגימה הינה חיונית אפוא בכדי לאמוד את מרווח הטעות ולפרש את תוצאות הסקר בהקשר של ציבור הבוחרים הגדול יותר.
חברות לוקחות לעתים קרובות חבילות גדולות של מוצרים כדי לבדוק את איכותם. התפלגות הדגימה מסייעת בקביעת הסבירות שהחבילה כולה עומדת בתקני איכות בהתבסס על תוצאות המדגם.
חוקרים עשויים לאסוף דגימות ממקומות ספציפיים כדי להעריך את רמות הזיהום. התפלגות הדגימה מודיעה להם על רמות הזיהום הסבירות על פני שטח רחב יותר.
חברות דוגמות לעתים קרובות תת-קבוצה של צרכנים כדי לבדוק תגובות למוצר או פרסומת חדשה. המשוב ממדגם זה אשר מנותח בהקשר של התפלגות הדגימה, עוזר לחזות את תגובת השוק הרחב יותר.
